题目内容
已知二次函数f（x）=x2-2x+a，a∈R
（1）求不等式f（x）≥f（a）的解；
（2）若af（x）-a2+3＞0对一切x∈R恒成立，求a的取值范围．
（1）求不等式f（x）≥f（a）的解；
（2）若af（x）-a2+3＞0对一切x∈R恒成立，求a的取值范围．
考点：函数恒成立问题,二次函数的性质
专题：综合题,函数的性质及应用
分析：（1）f（x）≥f（a）可化为（x-a）[x-（2-a）]≥0，按照两根2-a与a的大小关系分三种情况讨论即可；
（2）af（x）-a2+3＞0即为ax2-2ax+3＞0恒成立，a=0时易求解；a≠0时借助二次函数图象可得
，解出即可；
（2）af（x）-a2+3＞0即为ax2-2ax+3＞0恒成立，a=0时易求解；a≠0时借助二次函数图象可得
|
解答：
解：（1）f（x）≥f（a）即x2-2x+a≥a2-2a+a，亦即（x-a）[x-（2-a）]≥0，
①当2-a=a，即a=1时，不等式为（x-1）2≥0，解集为R；
②当2-a＞a，即a＜1时，不等式的解为{x|x≤a或x≥2-a}；
③当2-a＜a，即a＞1时，不等式的解为{x|x≤2-a或x≥a}；
综上所述，当a=1时，不等式的解集为R；当a＜1时，不等式的解集为{x|x≤a或x≥2-a}；当a＞1时，不等式的解集为{x|x≤2-a或x≥a}；
（2）af（x）-a2+3＞0即为ax2-2ax+3＞0恒成立，
当a=0时，不等式为3＞0恒成立；
当a≠0时，有
，解得0＜a＜3；
综上，a的取值范围是0≤a＜3．
①当2-a=a，即a=1时，不等式为（x-1）2≥0，解集为R；
②当2-a＞a，即a＜1时，不等式的解为{x|x≤a或x≥2-a}；
③当2-a＜a，即a＞1时，不等式的解为{x|x≤2-a或x≥a}；
综上所述，当a=1时，不等式的解集为R；当a＜1时，不等式的解集为{x|x≤a或x≥2-a}；当a＞1时，不等式的解集为{x|x≤2-a或x≥a}；
（2）af（x）-a2+3＞0即为ax2-2ax+3＞0恒成立，
当a=0时，不等式为3＞0恒成立；
当a≠0时，有
|
综上，a的取值范围是0≤a＜3．
点评：本题考查二次不等式的求解、函数恒成立问题，属中档题．深刻理解“三个二次”间的关系是解题关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
设f（x）=
，若f（0）是f（x）的最小值，则a的取值范围为（ ）
|
| A、[-1，2] |
| B、[-1，0] |
| C、[1，2] |
| D、[0，2] |
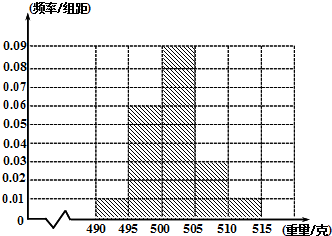某食品厂为了检查甲乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图．