题目内容
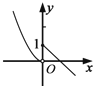
6. 已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ≤$\frac{π}{2}$)的图象如图所示,若函数g(x)=3[f(x)]3-4f(x)+m在x$∈[-\frac{π}{2},\frac{π}{2}]$上有4个不同的零点,则实数m的取值范围是[$\frac{13}{8}$,$\frac{16}{9}$].
已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ≤$\frac{π}{2}$)的图象如图所示,若函数g(x)=3[f(x)]3-4f(x)+m在x$∈[-\frac{π}{2},\frac{π}{2}]$上有4个不同的零点,则实数m的取值范围是[$\frac{13}{8}$,$\frac{16}{9}$].
分析 利用由y=Asin(ωx+φ)的部分图象可求得A,T,从而可得ω,又曲线经过($\frac{2π}{3}$,0),|φ|<$\frac{π}{2}$,可得φ的值,从而可求函数f(x)的解析式,将函数进行换元,转化为一元二次函数问题,由导数求出单调区间,结合函数f(x)的图象,即可确定m的取值范围.
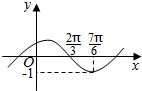
解答 解:由图知T=4($\frac{7π}{6}$-$\frac{2π}{3}$)=2π,
∴ω=1,
∴f(x)=sin(x+φ),
∵f($\frac{2π}{3}$)=0,
∴$\frac{2π}{3}$+φ=kπ,k∈Z.
∴φ=kπ-$\frac{2π}{3}$,k∈Z.
又|φ|≤$\frac{π}{2}$,
∴φ=$\frac{π}{3}$,
∴函数f(x)的解析式为:f(x)=sin(x+$\frac{π}{3}$).
由f(x)的图象可知,对于f(x)∈[$\frac{1}{2}$,1)上的每一个值,对应着[-$\frac{π}{2}$,$\frac{π}{2}$]上的两个x值,
又g(x)=3[f(x)]3-4f(x)+m=0,?m=-3[f(x)]3+4f(x)有4个不同的零点,
令f(x)=t,则m=-3t3+4t.
∵m′=-9t2+4=-9(t+$\frac{2}{3}$)(t-$\frac{2}{3}$),
∴m=-3t3+4t在[$\frac{1}{2}$,$\frac{2}{3}$]上单调递增,在[$\frac{2}{3}$,1]上单调递减,
而当t=$\frac{1}{2}$时,m=$\frac{13}{8}$;当t=$\frac{2}{3}$时,m=$\frac{16}{9}$;当t=1时,m=1,
结合图象可知,对于m∈[$\frac{13}{8}$,$\frac{16}{9}$]上的每一个值,对应着t=f(x)∈[$\frac{1}{2}$,1)上的两个值,进而对应着[-$\frac{π}{2}$,$\frac{π}{2}$]上的4个x值.
故答案为:[$\frac{13}{8}$,$\frac{16}{9}$].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求φ的值是关键,也是难点,考查识图与运算求解能力,此外还考查了复合函数零点的个数,一元二次方程的实根分布,以及换元法和数形结合法的解题思想,属于基本知识的考查.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
| A. | ?x>0,2x>x2 | B. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | ||
| C. | “a>b“是“ac2>bc2”的充要条件 | D. | “ab>1”是“a>1,b>1”的必要条件 |
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
| A. | $\frac{\sqrt{2}}{4}$ | B. | 64 | C. | 2$\sqrt{2}$ | D. | $\frac{1}{64}$ |
| A. | 600 | B. | 450 | C. | 300 | D. | 150 |
| A. | an+an+3>an+1+an+2 | B. | an+an+3=an+1+an+2 | ||
| C. | an+an+3<an+1+an+2 | D. | 与公比q有关 |