题目内容
14.下列命题中,真命题的是( )| A. | ?x>0,2x>x2 | B. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | ||
| C. | “a>b“是“ac2>bc2”的充要条件 | D. | “ab>1”是“a>1,b>1”的必要条件 |
分析 根据含有量词的命题的定义进行判断即可.
解答 解:A.若x=3,则23=8,32=9,此时2x>x2不成立,故A错误,
B.∵?x∈R,ex>0,∴?x0∈R,e${\;}^{{x}_{0}}$≤0不成立,故B错误,
C.当c=0,当a>b时,“ac2>bc2”不成立,即“a>b“是“ac2>bc2”的充要条件错误,故C错误,
D.当a>1,b>1时,ab>1成立,即“ab>1”是“a>1,b>1”的必要条件成立,故D正确,
故选:D
点评 本题主要考查含有量词的命题的判断,根据特称命题和全称命题的定义是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
5.若点P是曲线y2=4x上的一个动点,则点P到点A(0,1)的距离与点P到y轴的距离之和的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\sqrt{2}+1$ | D. | 2 |
9.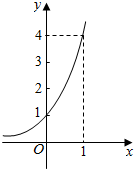 给出以下命题:
给出以下命题:
(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
 给出以下命题:
给出以下命题:(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
| A. | (1)(2)(3) | B. | (1)(3)(5) | C. | (2)(4)(5) | D. | (1)(3)(4) |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,且a2=b2+c2-bc,则△ABC的面积S的最大值为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\sqrt{3}$ |
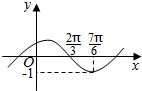 已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ≤$\frac{π}{2}$)的图象如图所示,若函数g(x)=3[f(x)]3-4f(x)+m在x$∈[-\frac{π}{2},\frac{π}{2}]$上有4个不同的零点,则实数m的取值范围是[$\frac{13}{8}$,$\frac{16}{9}$].
已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ≤$\frac{π}{2}$)的图象如图所示,若函数g(x)=3[f(x)]3-4f(x)+m在x$∈[-\frac{π}{2},\frac{π}{2}]$上有4个不同的零点,则实数m的取值范围是[$\frac{13}{8}$,$\frac{16}{9}$].