题目内容
11．已知幂函数f（x）的图象过点（4，$\frac{1}{2}$），则f（8）的值为（ ）| A． | $\frac{\sqrt{2}}{4}$ | B． | 64 | C． | 2$\sqrt{2}$ | D． | $\frac{1}{64}$ |
分析 幂函数f（x）=xa的图象过点（4，$\frac{1}{2}$），得到α的值，得到函数的解析式，再代入值计算即可．
解答 解：∵幂函数f（x）=xa的图象过点（4，$\frac{1}{2}$），
∴$\frac{1}{2}$=4α，
∴α=-$\frac{1}{2}$，
∴f（x）=${x}^{-\frac{1}{2}}$，
∴f（8）=${8}^{-\frac{1}{2}}$=$\frac{\sqrt{2}}{4}$
故选：A．
点评 本题考查了幂函数的解析式和函数值，属于基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
19．在△ABC中，角A，B，C所对的边分别为a，b，c，若a=$\sqrt{3}$，且a2=b2+c2-bc，则△ABC的面积S的最大值为（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{3\sqrt{3}}{4}$ | D． | $\sqrt{3}$ |
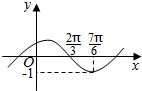已知函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$≤φ≤$\frac{π}{2}$）的图象如图所示，若函数g（x）=3[f（x）]3-4f（x）+m在x$∈[-\frac{π}{2}，\frac{π}{2}]$上有4个不同的零点，则实数m的取值范围是[$\frac{13}{8}$，$\frac{16}{9}$]．
16．函数f（x）=sin（x+$\frac{π}{4}$）图象的一条对称轴方程为（ ）
| A． | x=-$\frac{π}{4}$ | B． | x=$\frac{π}{4}$ | C． | x=$\frac{π}{2}$ | D． | x=π |