题目内容
已知向量
=(2cosα,2sinα),
=(2sinβ,2cosβ),|
+
|=
,则sin(α+β)的值为( )
| m |
| n |
| m |
| n |
8
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数,平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:由已知向量求出向量m,n的数量积和模,将|
+
|=
两边平方,再由两角和的正弦公式,即可得到.
| m |
| n |
8
| ||
| 5 |
解答:
解:∵向量
=(2cosα,2sinα),
=(2sinβ,2cosβ),|
+
|=
,
∴
•
=4(cosαsinβ+sinαcosβ)=4sin(α+β),|
|=|
|=2,
∴|
+
|2=
,即
2+2
•
+
2=
,
∴4+8sin(α+β)+4=
,
∴sin(α+β)=
.
故选B.
| m |
| n |
| m |
| n |
8
| ||
| 5 |
∴
| m |
| n |
| m |
| n |
∴|
| m |
| n |
| 64 |
| 5 |
| m |
| m |
| n |
| n |
| 64 |
| 5 |
∴4+8sin(α+β)+4=
| 64 |
| 5 |
∴sin(α+β)=
| 3 |
| 5 |
故选B.
点评:本题考查两角和的正弦公式的逆用,考查平面向量的数量积的坐标表示和性质,向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
班级与成绩的2×2列联表,表中数据m,n,p,q的值应分别为( )
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | p |
| 总计 | m | n | q |
| A、17,73,45,90 |
| B、17,90,73,45 |
| C、73,17,45,90 |
| D、73,45,90,17 |
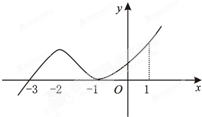 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3数y=f(x)的极值点;
②-1函数y=f(x)的最小值;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
过点P(1,3)的动直线l与圆x2+y2=3交于不同两点、B,在线段AB上取一点Q,满足
=-λ
,
=λ
,λ≠0且λ≠±1,则点Q所在的直线的方程为( )
| AP |
| PB |
| AQ |
| QB |
| A、x-3y=3 |
| B、x-y=3 |
| C、x+y=3 |
| D、x+3y=3 |
等差数列的前n项和为Sn,而且2Sn=2k+n2+n,则常数k的值为( )
| A、1 | B、-1 | C、1 | D、0 |
下列命题是真命题的是( )
| A、?x∈R,x>0 |
| B、?x∈R,x02+2x0+3=0 |
| C、有的三角形是正三角形 |
| D、每一个四边形都有外接圆 |
以下四种化简过程,其中正确的有( )个.
①sin(360°+200°)=sin200°
②sin(180°-200°)=-sin200°
③sin(180°+200°)=sin200°
④sin(-200°)=sin200°.
①sin(360°+200°)=sin200°
②sin(180°-200°)=-sin200°
③sin(180°+200°)=sin200°
④sin(-200°)=sin200°.
| A、1 | B、2 | C、3 | D、4 |
函数y=3sin(
-x)-cos(
+x),(x∈R)的最小值等于( )
| π |
| 3 |
| π |
| 6 |
| A、-3 | ||
| B、-2 | ||
| C、-1 | ||
D、-
|
函数f(x)=1+
(-2≤x≤2)与函数g(x)=m(x-2)+4.若函数h(x)=f(x)-g(x)有两个零点时,参数m的取值范围为( )
| 4-x2 |
A、[
| ||||
B、(-
| ||||
C、[
| ||||
D、(
|