题目内容
1．
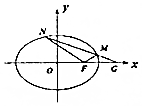已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），其短轴为2，离心率为$\frac{\sqrt{2}}{2}$．（Ⅰ）求椭圆E的方程；
（Ⅱ）设椭圆E的右焦点为F，过点G（2，0）作斜率不为0的直线交椭圆E于M，N两点，设直线FM和FN的斜率为k1，k2，试判断k1+k2是否为定值，若是定值，求出该定值；若不是定值，请说明理由．
分析 （Ⅰ）由椭圆的性质2b=2，离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$，求得a，求得椭圆方程；
（Ⅱ）设直线方程，代入椭圆方程，利用韦达定理及直线的斜率公式，即可求得k1+k2的值．
解答 解：（Ⅰ）由题意可知：2b=2，b=1，
椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$，
则a=$\sqrt{2}$，
∴椭圆的标准方程：$\frac{{x}^{2}}{2}+{y}^{2}=1$；
（Ⅱ）设直线MN的方程为y=k（x-2）（k≠0）．
$\left\{\begin{array}{l}{y=k（x-2）}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$，消去y整理得：（1+2k2）x2-8k2x+8k2-2=0．设M（x1，y1），N（x2，y2），
则x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$，x1x2=$\frac{8{k}^{2}-2}{1+2{k}^{2}}$，
k1+k2=$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$=$\frac{k（{x}_{1}-2）}{{x}_{1}-1}$+$\frac{k（{x}_{2}-2）}{{x}_{2}-1}$=k[2-$\frac{{x}_{1}+{x}_{2}-2}{{x}_{1}{x}_{2}-（{x}_{1}+{x}_{2}）+1}$]
=k[2-$\frac{\frac{8{k}^{2}}{1+2{k}^{2}}-2}{\frac{8{k}^{2}-2}{1+2{k}^{2}}-\frac{8{k}^{2}}{1+2{k}^{2}}+1}$]=0
∴k1+k2=0为定值．
点评 本题考查椭圆的标准方程及简单几何性质，直线与椭圆的位置关系，韦达定理及直线的斜率公式，考查计算能力，属于中档题．
学业测评一课一测系列答案
如图，在△ABC中，AB=BC=$\sqrt{6}$，∠ABC=90°，点D为AC的中点，将△ABD沿BD折起到△PBD的位置，使PC=PD，连接PC，得到三棱锥P-BCD，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）| A． | π | B． | 3π | C． | 5π | D． | 7π |
| A． | g（π）＜g（3）＜g（$\sqrt{2}$） | B． | g（π）＜g（$\sqrt{2}$）＜g（3） | C． | g（$\sqrt{2}$）＜g（3）＜g（π） | D． | g（$\sqrt{2}$）＜g（π）＜g（3） |
| A． | 12 | B． | 18 | C． | 24 | D． | 36 |
某校在一次高三年级“诊断性”测试后，对该年级的500名考生的成绩进行统计分析，成绩的频率分布表及频率分布直方图如图所示，规定成绩不小于130分为优秀．（1）若用分层抽样的方法从这500人中抽取5人的成绩进行分析，求其中成绩为优秀的学生人数；
（2）在（1）中抽取的5名学生中，要随机抽取2名学生参加分析座谈会，求恰有1人成绩为优秀的概率．
| 区间 | 人数 |
| [115，120） | 25 |
| [120，125） | a |
| [125，130） | 175 |
| [130，135） | 150 |
| [135，140） | b |