题目内容
9.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为3$\sqrt{2}$的正方形,AA1=3,E是线段A1B1上一点,若二面角A-BD-E的正切值为3,则三棱锥A-A1D1E外接球的表面积为35π.分析 如图所示,求出三棱锥A-A1D1E外接球的直径为$\sqrt{35}$,问题得以解决.
解答 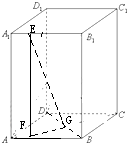 解:过点E作EF∥AA1交AB于F,过F作FG⊥BD于G,连接EG,
解:过点E作EF∥AA1交AB于F,过F作FG⊥BD于G,连接EG,
则∠EGF为二面角A-BD-E的平面角,
∵tan∠EGF=3,
∴$\frac{EF}{A{A}_{1}}$=3,
∵EF=AA1=3,
∴FG=1,
则BF=$\sqrt{2}$=B1E,
∴A1E=2$\sqrt{2}$,
则三棱锥A-A1D1E外接球的直径为$\sqrt{8+9+18}$=$\sqrt{35}$,
则其表面积为35π,
故答案为:35π
点评 本题考查了长方体和球体的几何体的性质,以及球的表面积公式,关键是求出球的直径,属于中档题.

练习册系列答案
相关题目
17.在数列{an}中,已知a1=3,且数列{an+(-1)n}是公比为2的等比数列,对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,则实数λ的取值范围是( )
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
18.执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为( )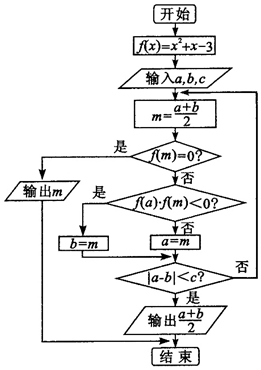

| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
19.现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是180.
| 纤维长度 | 频数 |
| [22.5,25.5) | 3 |
| [25.5,28.5) | 8 |
| [28.5,31.5) | 9 |
| [31.5,34.5) | 11 |
| [34.5,37.5) | 10 |
| [37.5,40.5) | 5 |
| [40.5,43.5] | 4 |
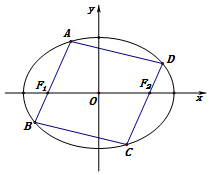 已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,左、右焦点分别是F1、F2,在椭圆E上有一动点A,过A、F1作一个平行四边形,使顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,左、右焦点分别是F1、F2,在椭圆E上有一动点A,过A、F1作一个平行四边形,使顶点A、B、C、D都在椭圆E上,如图所示.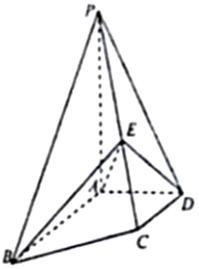 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC. 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.