题目内容
12．
如图，在△ABC中，AB=BC=$\sqrt{6}$，∠ABC=90°，点D为AC的中点，将△ABD沿BD折起到△PBD的位置，使PC=PD，连接PC，得到三棱锥P-BCD，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）| A． | π | B． | 3π | C． | 5π | D． | 7π |
分析 由题意得该三棱锥的面PCD是边长为$\sqrt{3}$的正三角形，且BD⊥平面PCD，求出三棱锥P-BDC外接球半径R=$\frac{\sqrt{7}}{2}$，由此能示出该球的表面积．
解答 解：由题意得该三棱锥的面PCD是边长为$\sqrt{3}$的正三角形，
且BD⊥平面PCD，
设三棱锥P-BDC外接球的球心为O，
△PCD外接圆的圆心为O1，则OO1⊥面PCD，
∴四边形OO1DB为直角梯形，
由BD=$\sqrt{3}$，O1D=1，及OB=OD，得OB=$\frac{\sqrt{7}}{2}$，
∴外接球半径为R=$\frac{\sqrt{7}}{2}$，
∴该球的表面积S=4πR2=4$π×\frac{7}{4}$=7π．
故选：D．
点评 本题考查球的表面积的求法，是中档题，解题时要认真审题，注意三棱锥的外接球的性质的合理运用．
练习册系列答案
相关题目
3．
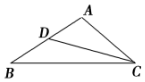如图所示，给出下列条件：
①∠B=∠ACD；
②∠ADC=∠ACB；
③$\frac{AC}{CD}$=$\frac{AB}{BC}$；
④AC2=AD•AB．
其中能够单独判定△ABC∽△ACD的个数为（ ）
如图所示，给出下列条件：①∠B=∠ACD；
②∠ADC=∠ACB；
③$\frac{AC}{CD}$=$\frac{AB}{BC}$；
④AC2=AD•AB．
其中能够单独判定△ABC∽△ACD的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
17．在数列{an}中，已知a1=3，且数列{an+（-1）n}是公比为2的等比数列，对于任意的n∈N*，不等式a1+a2+…+an≥λan+1恒成立，则实数λ的取值范围是（ ）
| A． | $（{-∞，\frac{2}{5}}]$ | B． | $（{-∞，\frac{1}{2}}]$ | C． | $（{-∞，\frac{2}{3}}]$ | D． | （-∞，1] |
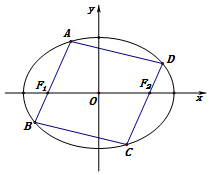已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，左、右焦点分别是F1、F2，在椭圆E上有一动点A，过A、F1作一个平行四边形，使顶点A、B、C、D都在椭圆E上，如图所示．
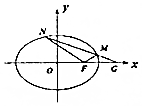已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），其短轴为2，离心率为$\frac{\sqrt{2}}{2}$．
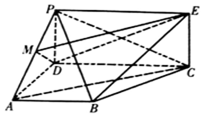如图，四边形PDCE为矩形，四边形ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=$\frac{1}{2}$CD=1．