题目内容
6.已知函数f(x)=ax(a>0,a≠1)的反函数的图象经过点($\frac{\sqrt{2}}{2}$,$\frac{1}{2}$).若函数g(x)的定义域为R,当x∈[-2,2]时,有g(x)=f(x),且函数g(x+2)为偶函数,则下列结论正确的是( )| A. | g(π)<g(3)<g($\sqrt{2}$) | B. | g(π)<g($\sqrt{2}$)<g(3) | C. | g($\sqrt{2}$)<g(3)<g(π) | D. | g($\sqrt{2}$)<g(π)<g(3) |
分析 根据函数的奇偶性,推导出g(-x+2)=g(x+2),再利用当x∈[-2,2]时,g(x)单调递减,即可求解.
解答 解:函数f(x)=ax(a>0,a≠1)的反函数的图象经过点($\frac{\sqrt{2}}{2}$,$\frac{1}{2}$),则a=$\frac{1}{2}$,
∵y=g(x+2)是偶函数,∴g(-x+2)=g(x+2),
∴g(3)=g(1),g(π)=f(4-π),
∵4-π<1<$\sqrt{2}$,当x∈[-2,2]时,g(x)单调递减,
∴g(4-π)>g(1)>g($\sqrt{2}$),
∴g($\sqrt{2}$)<g(3)<g(π),
故选C.
点评 本题考查反函数,考查函数单调性、奇偶性,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
17.在数列{an}中,已知a1=3,且数列{an+(-1)n}是公比为2的等比数列,对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,则实数λ的取值范围是( )
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
18.执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为( )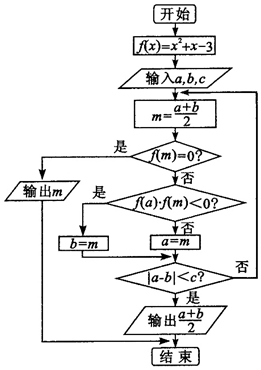

| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
15.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1536石,验得米内夹谷,抽样取米一把,数得224粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 169石 | B. | 192石 | C. | 1367石 | D. | 1164石 |
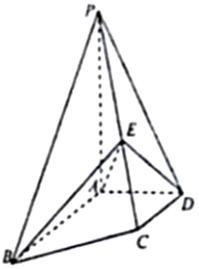 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.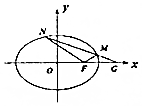 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.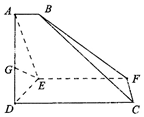 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.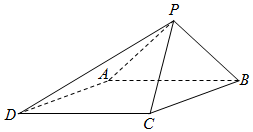 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.