题目内容
11.点P为正四面体ABCD的棱BC上任意一点,则直线AP与直线DC所成角的范围是$[\frac{π}{3},\frac{π}{2}]$.分析 利用两个极限位置,求出直线AP与直线DC所成角,即可得出结论.
解答 解:由题意,P在B处,直线AP与直线DC所成角为$\frac{π}{2}$,
P在C处,直线AP与直线DC所成角为$\frac{π}{3}$,
故答案为$[\frac{π}{3},\frac{π}{2}]$.
点评 本题考查直线与直线所成角,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
19.现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是180.
| 纤维长度 | 频数 |
| [22.5,25.5) | 3 |
| [25.5,28.5) | 8 |
| [28.5,31.5) | 9 |
| [31.5,34.5) | 11 |
| [34.5,37.5) | 10 |
| [37.5,40.5) | 5 |
| [40.5,43.5] | 4 |
6.若平面α,β,γ中,α⊥β,则“γ⊥β”是“α∥γ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知抛物线C:y2=8x,直线l:y=$\frac{{\sqrt{3}}}{3}$(x-2),直线l交C于A,B两点,则|AB|等于( )
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
20.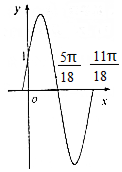 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
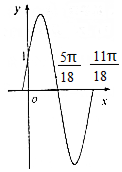 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
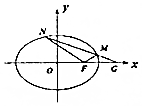 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.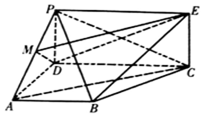 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.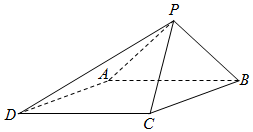 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.