题目内容
8．设向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，若$\overrightarrow{a}$=（3，-1），$\overrightarrow{b}$-$\overrightarrow{a}$=（-1，1），则cosθ=$\frac{3\sqrt{10}}{10}$．分析 根据向量的坐标运算和向量的夹角公式计即可．
解答 解：∵$\overrightarrow{a}$=（3，-1），$\overrightarrow{b}$-$\overrightarrow{a}$=（-1，1），
∴$\overrightarrow{b}$=（2，0），
∴|$\overrightarrow{a}$|=$\sqrt{10}$，|$\overrightarrow{b}$|=2，$\overrightarrow{a}•\overrightarrow{b}$=6，
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a|}•|\overrightarrow{b}|}$=$\frac{6}{2\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$，
故答案为：$\frac{3\sqrt{10}}{10}$．
点评 考查向量坐标的数乘和减法运算，向量坐标的数量积的运算，以及向量夹角的余弦公式．
练习册系列答案
备战中考寒假系列答案
相关题目
18．若双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的中心在坐标原点O，过C的右顶点和右焦点分别作垂直于x轴的直线，交C的渐近线于A，B和M，N，若△OAB与△OMN的面积之比为1：4，则C的渐近线方程为（ ）
| A． | y=±x | B． | $y=±\sqrt{3}x$ | C． | y=±2x | D． | y=±3x |
3．在△ABC中，角A，B，C的对边分别为a，b，c，且$\frac{cosB}{b}$=-$\frac{3cosC}{c}$，则角A的最大值是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
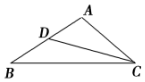如图所示，给出下列条件：
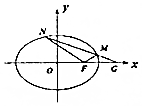已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），其短轴为2，离心率为$\frac{\sqrt{2}}{2}$．