题目内容
若函数f(x)=
，则f[f（e）]（e为自然对数的底数）=（ ）
|
| A、0 |
| B、1 |
| C、2 |
| D、ln（e2+1） |
考点：函数的值
专题：函数的性质及应用
分析：根据分段函数的表达式直接代入进行求值即可．
解答：
解：∵函数f(x)=
，
∴f（e）=lne=1，
则f[f（e）]=f（1）=1+1=2，
故选：C．
|
∴f（e）=lne=1，
则f[f（e）]=f（1）=1+1=2，
故选：C．
点评：本题主要考查函数值的计算，直接利用分段函数的表达式进行求值即可．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
某人先朝正东方向走了xkm，再朝西偏北30°的方向走了3km，结果它离出发点恰好为
km，那么x等于（ ）
| 3 |
A、
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
若直线ax+y+1=0与圆x2+y2-2x=0相切，则a的值为（ ）
| A、±1 | B、±2 | C、-1 | D、0 |
若不等式ax2+bx+c≥0的解集是{x|-1≤x≤2}，则不等式cx2+bx+a＜0的解集是（ ）
A、（-∞，-1）∪（
| ||
B、（-
| ||
C、（-∞，-
| ||
D、（-1，
|
已知命题P：?x∈R，x2+2ax+a≤0．若命题P是假命题，则实数a的取值范围是（ ）
| A、（0，1） |
| B、（-∞，0）∪（1，+∞） |
| C、[0，1] |
| D、（-∞，0）∪[1，+∞） |
已知x∈（2kπ-
π，2kπ+
）（k∈Z），且cos(
-x)=-
，则cos2x的值是（ ）
| 3 |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
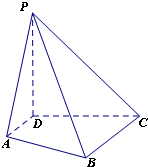在四棱锥P-ABCD中，PD⊥平面ABCD，PD=CD=BC=2AD，AD∥BC，∠BCD=90°．