Question

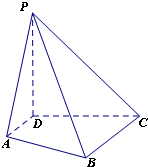在四棱锥P-ABCD中，PD⊥平面ABCD，PD=CD=BC=2AD，AD∥BC，∠BCD=90°．
（Ⅰ）求证：BC⊥PC；
（Ⅱ）求PA与平面PBC所成角的正弦值；
（Ⅲ）线段PB上是否存在点E，使AE⊥平面PBC？说明理由．

Answer 1

考点：用空间向量求直线与平面的夹角,直线与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算

专题：空间位置关系与距离,空间角,空间向量及应用

分析：（Ⅰ）通过证明BC⊥平面PCD，然后证明BC⊥PC；
（Ⅱ）通过建立空间直角坐标系，求出设平面PBC的法向量，然后求解PA与平面PBC所成角的正弦值；
（Ⅲ）法一：当E为线段PB的中点时，AE⊥平面PBC．分别取PB，PC的中点E，F，连结AE，DF，EF．
证明四边形AEFD是平行四边形．然后证明AE⊥平面PBC．即可推出线段PB上是否存在点E，使AE⊥平面PBC．
法二，利用空间直角坐标系，通过向量共线，求出点的坐标即可．

解答： （本小题满分14分）
证明：（Ⅰ）在四棱锥P-ABCD中，
∵PD⊥平面ABCD，BC?平面ABCD，
∴PD⊥BC．
∵∠BCD=90°，
∴BC⊥CD．
∵PD∩DC=D，
∴BC⊥平面PCD．
∵PC?平面PCD，
∴BC⊥PC．…（4分）
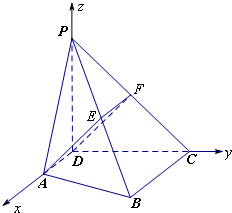
（Ⅱ） 如图，以D为原点建立空间直角坐标系D-xyz．
不妨设AD=1，则PD=CD=BC=2．
则D（0，0，0），A（1，0，0），B（2，2，0），C（0，2，0），P（0，0，2）．
∴

PA

=(1，0，-2)，

PB

=(2，2，-2)，

PC

=(0，2，-2)．
设平面PBC的法向量

n

=（x，y，z）．
∴

n • PB =0 n • PC =0

．即

2x+2y-2z=0 2y-2z=0

．
令y=1，则x=0，z=1．
∴n=（0，1，1）
∴cos＜

PA

，n＞=

-2

5 • 2

=-

10

5

∴PA与平面PBC所成角的正弦值为

10

5

．…（9分）
（Ⅲ）（法一）当E为线段PB的中点时，AE⊥平面PBC．
如图：分别取PB，PC的中点E，F，连结AE，DF，EF．
∴EF∥BC，且EF=

1

2

BC．
∵AD∥BC，且AD=

1

2

BC，
∴AD∥EF，且AD=EF．
∴四边形AEFD是平行四边形．
∴AE∥DF．
∵PD=CD，
∴三角形PCD是等腰三角形．
∴DF⊥PC．
∵BC⊥平面PCD，
∴DF⊥BC．
∵PC∩BC=C，
∴DF⊥平面PBC．
∴AE⊥平面PBC．
即在线段PB上存在点E，使AE⊥平面PBC．
（法二）设在线段PB上存在点E，当

PE

=λ

PB

(0＜λ＜1)时，AE⊥平面PBC．
设E（x₀，y₀，z₀），则

PE

=(x0，y0，z0-2)．
∴（x₀，y₀，z₀-2）=λ（2，2，-2）．
即x₀=2λ，y₀=2λ，z₀=-2λ+2．
∴E（2λ，2λ，-2λ+2）．
∴

AE

=(2λ-1，2λ，-2λ+2)．
由（Ⅱ）可知平面PBC的法向量

n

=（0，1，1）．
若AE⊥平面PBC，

AE

∥

n

．
即

AE

=μ

n

．
解得λ=

1

2

，μ=1．
∴当

PE

=

1

2

PB

，即E为PB中点时，AE⊥平面PBC．…（14分）

点评：本题考查空间点的坐标的求法，直线与平面所成的角的求法，直线与平面垂直的判断与性质的应用，考查空间想象能力以及逻辑推理能力．