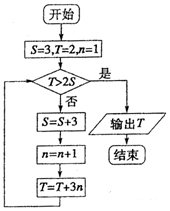
题目内容
4.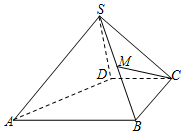 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.(Ⅰ)证明:CD⊥SD;
(Ⅱ)证明:CM∥面SAD.
分析 (I)由SD⊥面SAB得出SD⊥AB,结合AB∥CD即可得出CD⊥SD;
(II)取SA的中点N,连结ND,MN,利用中位线定理证明四边形MNDC是平行四边形,故而CM∥DN,于是CM∥面SAD.
解答 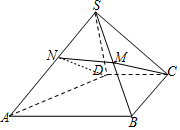 证明:(I)∵SD⊥面SAB,AB?平面SAB,
证明:(I)∵SD⊥面SAB,AB?平面SAB,
∴SD⊥AB,
又∵AB∥CD,
∴SD⊥CD.
(II)取SA的中点N,连结ND,MN,
∵M是SB的中点,N是SA的中点,
∴MN$\stackrel{∥}{=}$$\frac{1}{2}$AB,又CD$\stackrel{∥}{=}$$\frac{1}{2}$AB,
∴MN$\stackrel{∥}{=}$CD,
∴四边形MNDC是平行四边形,
∴CM∥ND,
又CM?平面SAD,ND?平面SAD,
∴CM∥面SAD.
点评 本题考查了线面垂直的性质,线面平行的判定,属于基础题.

练习册系列答案
相关题目
12.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则a5等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
9.${∫}_{0}^{\frac{π}{6}}$cosxdx=${∫}_{1}^{a}$$\frac{1}{x}$dx(a>1),则a的值为( )
| A. | $\sqrt{e}$ | B. | 2 | C. | e | D. | 3 |
16.已知函数f(x)=2lnx-ax2+3,若存在实数m、n∈[1,5]满足n-m≥2时,f(m)=f(n)成立,则实数a的最大值为( )
| A. | $\frac{ln5-ln3}{8}$ | B. | $\frac{ln3}{4}$ | C. | $\frac{ln5+ln3}{8}$ | D. | $\frac{ln4}{3}$ |
14.已知函数f(x)为定义域在R上的奇函数,当x>0,f(x)=lnx-2x-f(1),则当x<0时,f(x)的表达式为( )
| A. | f(x)=ln(-x)+2x+1 | B. | f(x)=-ln(-x)-2x+1 | C. | f(x)=-ln(-x)-2x-1 | D. | f(x)=-ln(-x)+2x-1 |