题目内容
15.已知数列{an}满足a1=1,a2=3,an+2=(2+cosnπ)(an+1)-3(n∈N*).(1)求数列{an}的通项公式;
(2)令bn=$\left\{\begin{array}{l}\frac{{{{log}_3}{a_n}}}{{{n^2}({n+2})}},n=2k({k∈{N^*}})\\{a_n},n=2k-1({k∈{N^*}})\end{array}$,Tn为数列{bn}的前n项和,求Tn.
分析 (1)an+2=(2+cosnπ)(an+1)-3,n∈N*.当n=2k-1时,an+2=an-2,∴{a2k-1}是等差数列,首项为1,公差为-2.当n=2k时,an+2=3an,可得{a2k}是等比数列,首项为3,公比为3,即可得出.
(2)bn=$\left\{\begin{array}{l}\frac{{{{log}_3}{a_n}}}{{{n^2}({n+2})}},n=2k({k∈{N^*}})\\{a_n},n=2k-1({k∈{N^*}})\end{array}$,n=2k(k∈N*)时,bn=$\frac{1}{2n(n+2)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+2})$;n=2k-1(k∈N*)时,bn=2-n.对n分类讨论即可得出.
解答 解:(1)∵an+2=(2+cosnπ)(an+1)-3,n∈N*.
∴当n=2k-1时,an+2=an-2,∴{a2k-1}是等差数列,首项为1,公差为-2,
∴a2k-1=1-2(k-1)=3-2k,即n为奇数时an=2-n.
当n=2k时,an+2=3an,∴{a2k}是等比数列,首项为3,公比为3,
∴a2k=3×3k-1,即n为偶数时an=${3}^{\frac{n}{2}}$.
∴an=$\left\{\begin{array}{l}{2-n,n为奇数}\\{{3}^{\frac{n}{2}},n为偶数}\end{array}\right.$.
(2)bn=$\left\{\begin{array}{l}\frac{{{{log}_3}{a_n}}}{{{n^2}({n+2})}},n=2k({k∈{N^*}})\\{a_n},n=2k-1({k∈{N^*}})\end{array}$,
n=2k(k∈N*)时,bn=$\frac{1}{2n(n+2)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+2})$;
n=2k-1(k∈N*)时,bn=2-n.
∴n=2k(k∈N*)时,Tn=T2k=(b1+b3+…+b2k-1)+(b2+b4+…+b2k)
=$\frac{k(1+3-2k)}{2}$+$\frac{1}{4}[(\frac{1}{2}-\frac{1}{4})+(\frac{1}{4}-\frac{1}{6})$+…+$(\frac{1}{2k}-\frac{1}{2k+2})]$=2k-k2+$\frac{1}{4}$$(\frac{1}{2}-\frac{1}{2k+2})$=2k-k2+$\frac{k}{8k+8}$=$n-\frac{{n}^{2}}{4}$+$\frac{n}{8n+16}$.
n=2k-1(k∈N*)时,Tn=Tn-1+bn=$(n-1)-\frac{(n-1)^{2}}{4}$+$\frac{n-1}{8n+24}$+2-n=1-$\frac{(n-1)^{2}}{4}$+$\frac{n-1}{8n+24}$.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、裂项求和方法、分类讨论方法,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{3}{4}$ | B. | $\frac{4\sqrt{23}}{23}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{23}}{4}$ |
| 购买商品金额 | 折扣 |
| 消费不超过200元的部分 | 9折 |
| 消费超过200元但不超过500元的部分 | 8折 |
| 消费超过500元但不超过1000元的部分 | 7折 |
| 消费超过1000元的部分 | 6折 |
| 购买商品金额 | (0,200] | (200,500] | (500,1000] | 1000以上 |
| 人数 | 10 | 40 | 30 | 20 |
(Ⅱ)估算顾客实际消费金额y不超过180的概率;
(Ⅲ)估算顾客实际消费金额y超过420的概率.
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$-1 |
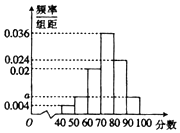 某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.
某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.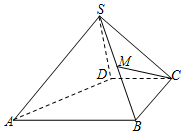 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.