题目内容
12.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则a5等于( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 利用已知条件逐步求解即可.
解答 解:4Sn=n(an+an+1),可得4S2=2(a2+a3),4S1=a1+a2,a2=3a1,a3=5a1,从而36a1=3(5a1+7),a1=1,
a2=3,a3=5,a4=7,4S4=4(a4+a5),解得a5=9.
故选:B.
点评 本题考查数列的递推关系式的应用,考查计算能力.

练习册系列答案
相关题目
3.直线$\sqrt{2}$ax+by=1与圆x2+y2=1相交于A、B两点(其中a、b是正实数),且△AOB是直角三角形(O是坐标原点),则$\frac{1}{ab}$的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$-1 |
20.若定义在R上的函数f(x)满足:(Ⅰ)f(x1+x2)=f(x1)•f(x2),(Ⅱ)?x1<x2,f(x1)>f(x2),则满足以上条件的一个函数解析式为y=($\frac{1}{3}$)x.
1.$\frac{3-2i}{1+3i}$=( )
| A. | -$\frac{3}{10}$-$\frac{11}{10}$i | B. | -$\frac{3}{10}$+$\frac{11}{10}$i | C. | $\frac{3}{10}$+$\frac{11}{10}$i | D. | $\frac{3}{10}$-$\frac{11}{10}$i |
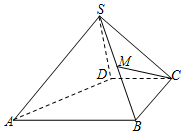 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD. 如图,矩形ABCD的边AB=8,BC=4,以CD为直径在矩形的外部作一半圆,圆心为O,过CD上一点N作AB的垂线交半圆弧于P,交AB于Q,M是曲线PDA上一动点.
如图,矩形ABCD的边AB=8,BC=4,以CD为直径在矩形的外部作一半圆,圆心为O,过CD上一点N作AB的垂线交半圆弧于P,交AB于Q,M是曲线PDA上一动点.