题目内容
16.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>a>0)的右焦点为F,O为坐标原点,若存在直线l过点F交双曲线C的右支于A,B两点,使$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则双曲线离心率的取值范围是$\sqrt{3}$>e≥$\frac{1+\sqrt{5}}{2}$.分析 设焦点为F(c,0),设直线AB:y=k(x-c),A(x1,y1),B(x2,y2),联立直线方程和双曲线方程,消去y,运用韦达定理和判别式大于0,由两直线垂直的条件:斜率之积为-1,可得k,即可得到离心率的范围.
解答 解:直线的斜率不存在时,A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$),由于OA⊥OB,则有x1x2+y1y2=0,可得e=$\frac{1+\sqrt{5}}{2}$;
焦点为F(c,0),直线AB:y=k(x-c),
设A(x1,y1),B(x2,y2),
则联立直线方程和双曲线的方程,可得
(b2-a2k2)x2+2ca2k2x-a2k2c2-a2b2=0,
则△=4c2a4k4+4(b2-a2k2)(a2k2c2+a2b2)>0,
x1+x2=$\frac{-2c{a}^{2}{k}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$,x1x2=$\frac{-{a}^{2}{k}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$,
则y1y2=k2(x1x2+c2-c(x1+x2))=k2•$\frac{{a}^{2}{b}^{2}-{b}^{2}{c}^{2}}{{a}^{2}{k}^{2}-{b}^{2}}$,
由于OA⊥OB,则有x1x2+y1y2=0,
即有a2b2+a2k2c2+k2(a2b2-b2c2)=0,
即有k2=$\frac{{a}^{2}{b}^{2}}{{b}^{4}-{a}^{4}-{a}^{2}{b}^{2}}$,
∴$\frac{{a}^{2}{b}^{2}}{{b}^{4}-{a}^{4}-{a}^{2}{b}^{2}}$>$\frac{{b}^{2}}{{a}^{2}}$,
∵b>a,∴$\sqrt{3}$>e>$\frac{1+\sqrt{5}}{2}$,
故答案为$\sqrt{3}$>e≥$\frac{1+\sqrt{5}}{2}$.
点评 本题考查双曲线的离心率的范围,考查联立直线方程和双曲线方程,消去未知数,运用韦达定理和判别式大于0,考查运算能力,属于中档题和易错题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |
| A. | 如果a1是5的倍数,那么数列{an}与数列{2n}必有相同的项 | |
| B. | 如果a1不是5的倍数,那么数列{an}与数列{2n}必没有相同的项 | |
| C. | 如果a1不是5的倍数,那么数列{an}与数列{2n}只有有限个相同的项 | |
| D. | 如果a1不是5的倍数,那么数列{an}与数列{2n}有无穷多个相同的项. |
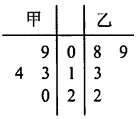 甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )| A. | v1>v2,s1>s2 | B. | v1<v2,s1>s2 | C. | v1>v2,s1<s2 | D. | v1<v2,s1<s2 |
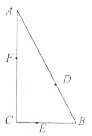 如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.
如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.