题目内容
3.已知函数f(x)=x2+ln23x-2a(x+3ln3x)+10a2,若存在x0使得$f({x_0})≤\frac{1}{10}$成立,则实数a的值为( )| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{30}$ |
分析 把函数f(x)可以看作是动点M(x,ln3x)与动点N(a,3a)之间距离的平方,利用导数求出曲线y=ln3x上与直线y=3x平行的切线的切点,得到曲线上点到直线距离的最小值,结合题意可得只有切点到直线距离的平方等于$\frac{1}{10}$,然后由两直线斜率的关系列式求得实数a的值.
解答 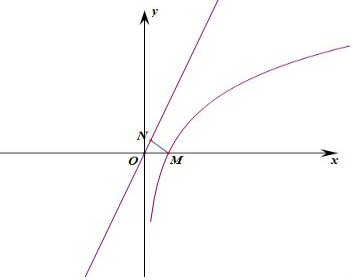 解:函数f(x)=x2+ln23x-2a(x+3ln3x)+10a2=(ln3x-3a)2+(x-a)2,
解:函数f(x)=x2+ln23x-2a(x+3ln3x)+10a2=(ln3x-3a)2+(x-a)2,
函数f(x)可以看作是动点M(x,ln3x)与动点N(a,3a)之间距离的平方,
动点M在函数y=ln3x的图象上,N在直线y=3x的图象上,
问题转化为求直线上的动点到曲线的最小距离,
由y=ln3x得,y'=$\frac{1}{x}$=3,解得x=$\frac{1}{3}$,
∴曲线上点M($\frac{1}{3}$,0)到直线y=3x的距离最小,
最小距离d=$\frac{1}{\sqrt{10}}$,
则f(x)≥$\frac{1}{10}$,
根据题意,要使f(x0)≤$\frac{1}{10}$,
则f(x0)=$\frac{1}{10}$,此时N恰好为垂足,
由kMN=$\frac{3a-0}{a-\frac{1}{3}}$=-$\frac{1}{3}$,
解得a=$\frac{1}{30}$.
故选:D.
点评 本题考查利用导数求曲线上过某点切线的斜率,考查了数形结合和数学转化思想方法,训练了点到直线的距离公式的应用,是中档题.

练习册系列答案
相关题目
13.方程($\frac{1}{3}$)x-x=0的解有( )
| A. | 0个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.某射击手射击一次命中的概率为0.8,连续两次均射中的概率是0.5,已知某次射中,则随后一次射中的概率是( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
13.函数y=$\sqrt{3}$sin2x+cos2x的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
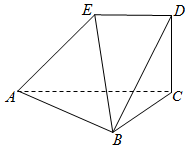 如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.
如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.