题目内容
三棱锥O-ABC的顶点在空间直角坐标系O-xyz中的坐标分别是O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),则点C到平面OAB的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:空间向量及应用
分析:求出法向量设
=(x,y,z),平面ABO的法向量,
,运用点C到平面OAB的距离为:
,求解即可.
| n |
|
|
| ||||
|
|
解答:
解:∵O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),
∴
=(1,0,1),
=(1,1,0),
=(0,1,1),
设
=(x,y,z),平面ABO的法向量,
∴
,
令x=1,y=-1,z=-1,
∴
=(1,-1,-1),
•
=-2,|
|=
∴点C到平面OAB的距离为:
=
=
,
故选:A
∴
| OA |
| OB |
| OC |
设
| n |
∴
|
令x=1,y=-1,z=-1,
∴
| n |
| n |
| OC |
| n |
| 3 |
∴点C到平面OAB的距离为:
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 3 |
故选:A
点评:本题考查了空间向量的运用求解空间距离问题,属于中档题,计算要准确.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列说法正确的是( )
| A、命题“若x=1则x2=1”的否命题为“若x2≠1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、“命题p,q中至少有一个为真命题”是“p或q为真命题”的充分不必要条件 |
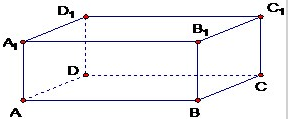 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).