题目内容
已知关于x的方程x2+ax+4=0.求下列条件下a的取值范围.
(1)若关于x的方程在[-1,5)上有解.
(2)若关于x的方程在[-1,5)上无解.
(3)若关于x的方程在[-1,5)上只有一解.
(4)若关于x的方程在[-1,5)有两个不同的实数解.
(1)若关于x的方程在[-1,5)上有解.
(2)若关于x的方程在[-1,5)上无解.
(3)若关于x的方程在[-1,5)上只有一解.
(4)若关于x的方程在[-1,5)有两个不同的实数解.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:由题意,令f(x)=x2+ax+4,从而可得对称轴为-
,开口向上,f(0)=4,△=a2-4×4=(a+4)(a-4);
(1)在△≥0的情况下按对称轴的位置讨论即可,故分三种情况讨论;
(2)由(1)可直接写出(2)中a的取值范围;
(3)在有解的条件下排除有两个不同的解,从而得到有一解的情况即可;
(4)由(3)直接写出即可.
| a |
| 2 |
(1)在△≥0的情况下按对称轴的位置讨论即可,故分三种情况讨论;
(2)由(1)可直接写出(2)中a的取值范围;
(3)在有解的条件下排除有两个不同的解,从而得到有一解的情况即可;
(4)由(3)直接写出即可.
解答:
解:令f(x)=x2+ax+4,
则有对称轴为-
,开口向上,f(0)=4,
△=a2-4×4=(a+4)(a-4);
(1)若使关于x的方程在[-1,5)上有解,
①若a≥4,则-
≤-2;
则f(-1)=1-a+4≤0,
解得a≥5,此时方程在[-1,5)上有一个解;
②若-10<a≤-4,则2≤-
<5,
则f(-
)=-
+4≤0,
即-10<a≤-4;
③若a≤-10,则-
≥5,
则f(5)=25+5a+4<0,
解得,a<-
,此时方程在[-1,5)上有一个解;
综上所述,a≥5或a≤-4;
(2)若使关于x的方程在[-1,5)上无解,
则-4<a<5;
(3)若使关于x的方程在[-1,5)上有两个不同的解,
则
解得,
-
<a<-4,
故关于x的方程在[-1,5)上只有一解时,
a≥5或a=-4或a≤-
;
(4)由(3)知,-
<a<-4.
则有对称轴为-
| a |
| 2 |
△=a2-4×4=(a+4)(a-4);
(1)若使关于x的方程在[-1,5)上有解,
①若a≥4,则-
| a |
| 2 |
则f(-1)=1-a+4≤0,
解得a≥5,此时方程在[-1,5)上有一个解;
②若-10<a≤-4,则2≤-
| a |
| 2 |
则f(-
| a |
| 2 |
| a2 |
| 4 |
即-10<a≤-4;
③若a≤-10,则-
| a |
| 2 |
则f(5)=25+5a+4<0,
解得,a<-
| 29 |
| 5 |
综上所述,a≥5或a≤-4;
(2)若使关于x的方程在[-1,5)上无解,
则-4<a<5;
(3)若使关于x的方程在[-1,5)上有两个不同的解,
则
|
-
| 29 |
| 5 |
故关于x的方程在[-1,5)上只有一解时,
a≥5或a=-4或a≤-
| 29 |
| 5 |
(4)由(3)知,-
| 29 |
| 5 |
点评:本题考查了二次函数的性质及图象,属于中档题.

练习册系列答案
相关题目
三棱锥O-ABC的顶点在空间直角坐标系O-xyz中的坐标分别是O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),则点C到平面OAB的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若O为△ABC所在平面内一点,且满足(
-
)•(
+
-2
)=0,则△ABC的形状为( )
| OC |
| OB |
| OB |
| OC |
| OA |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
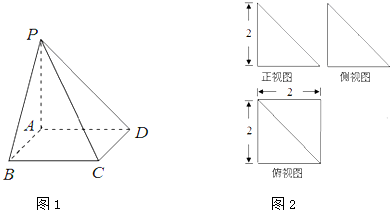
 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,PA⊥AB,PA⊥AD,且PA=AB=a,求异面直线PD与AC所成的角.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,PA⊥AB,PA⊥AD,且PA=AB=a,求异面直线PD与AC所成的角.