用反证法证明命题“设a.b是实数.则方程x3+ax+b=0至少有一个实根时.要做的反设是(1)方程x3+ax+b=0恰好有两个实根 (2)方程x3+ax+b=0至多有一个实根(3)方程x3+ax+b=0至多有两个实根 (4)方程x3+ax+b=0没有实根．题目和参考答案——青夏教育精英家教网——

题目内容

7．用反证法证明命题“设a，b是实数，则方程x³+ax+b=0至少有一个实根”时，要做的反设是（4）（填序号）
（1）方程x³+ax+b=0恰好有两个实根（2）方程x³+ax+b=0至多有一个实根
（3）方程x³+ax+b=0至多有两个实根（4）方程x³+ax+b=0没有实根．

分析直接利用命题的否定写出假设即可．

解答解：反证法证明问题时，反设实际是命题的否定，
∴用反证法证明命题“设a，b为实数，则方程x³+ax+b=0至少有一个实根”时，要做的假设是：方程x³+ax+b=0没有实根．
故答案为：（4）．

点评本题考查反证法证明问题的步骤，基本知识的考查．

练习册系列答案

中考大检阅系列答案

中考易系列答案

中考英语专项练习系列答案

中考英语词汇记忆与检测宝典系列答案

中考英语话题复习浙江工商大学出版社系列答案

中考指要系列答案

金牌1号名优测试卷系列答案

培生新课堂同步训练与单元测评系列答案

中考系列红十套系列答案

中考新方向系列答案

相关题目

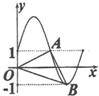
17．函数y=2sin$\frac{πx}{2}$+1的部分图象如图所示，则（${\overrightarrow{OA}$+2$\overrightarrow{OB}}$）•$\overrightarrow{AB}$=（　　）

18．已知椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞c）的离心率为$\frac{{\sqrt{2}}}{2}$，过焦点且垂直于x轴的直线被椭圆E截得的线段长为2．
（1）求椭圆E的方程；
（2）直线y=kx+1与椭圆E交于A，B两点，以AB为直径的圆与y轴正半轴交于点C．是否存在实数k，使得y轴恰好平分∠ACB？若存在，求出k的值；若不存在，请说明理由．

15．已知点O在平面ABC内，若$\overrightarrow{AO}$=λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$）（λ∈R），则直线AO经过△ABC的内心．

2．用反证法证明命题：“设实数a，b，c满足a+b+c=3，则a，b，c中至少有一个数不小于1”时，第一步应写：假设a，b，c都小于2．

12．已知：
1+$\frac{1}{2}$=$\frac{3}{2}$
1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$＞2
1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{7}$+$\frac{1}{8}$＞$\frac{5}{2}$
1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{7}$+$\frac{1}{8}$+$\frac{1}{9}$+…+$\frac{1}{16}$＞3
…
以此类推，写出一般的结论并加以证明．

19．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左顶点与抛物线y²=2px（p＞0）的焦点的距离为3，且双曲线的一条渐近线与抛物线的准线的交点坐标为（-1，-1），则双曲线的标准方程为（　　）

$\frac{x^2}{2}$-$\frac{y^2}{2}$=1

$\frac{x^2}{4}$-$\frac{y^2}{4}$=1

$\frac{x^2}{4}$-y²=1

$\frac{x^2}{2}$-y²=1

16．（1）已知p³+q³=2，求证p+q≤2，用反证法证明时，可假设p+q≥2，
（2）已知a，b∈R，|a|+|b|＜1，求证方程x²+ax+b=0的两根的绝对值都小于1．
用反证法证明时可假设方程至少有一根的绝对值大于或等于1．以下结论正确的是（　　）

	A．	（1）与（2）的假设都错误		B．	（1）与（2）的假设都正确
	C．	（1）的假设错误；（2）的假设正确		D．	（1）的假设正确；（2）的假设错误

17．不等式|2x-log₂x|＜2x+|log₂x|成立，则（　　）