题目内容
17．函数y=2sin$\frac{πx}{2}$+1的部分图象如图所示，则（${\overrightarrow{OA}$+2$\overrightarrow{OB}}$）•$\overrightarrow{AB}$=（ ）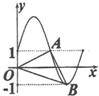
| A． | -10 | B． | -5 | C． | 5 | D． | 10 |
分析 根据根据函数$y=2sin\frac{πx}{2}+1$的部分图象，求得A、B的坐标，再利用两个向量的数量积公式求得要求式子的值．
解答 解：根据函数$y=2sin\frac{πx}{2}+1$的部分图象，可得sin$\frac{π}{2}$x=0，由五点作图法知$\frac{π}{2}$x=π，故x=2，∴A（2，1）．
令y=2sin$\frac{π}{2}$x+1=-1，求得sin$\frac{π}{2}$x=-1，求得x=3，故B（3，-1）．
∴$（{\overrightarrow{OA}+2\overrightarrow{OB}}）•\overrightarrow{AB}$=（8，-1）•（1，-2）=8+2=10，
故选：D．
点评 本题主要考查正弦函数的图象特征，两个向量的数量积公式的应用，属于基础题．
练习册系列答案
相关题目
5．已知函数f（x）=2cos（$\frac{π}{3}$x+φ）图象的一个对称中心为（2，0），且f（1）＞f（3），要得到函数，f（x）的图象可将函数y=2cos$\frac{π}{3}$x的图象（ ）
| A． | 向左平移$\frac{1}{2}$个单位长度 | B． | 向左平移$\frac{π}{6}$个单位长度 | ||
| C． | 向右平移$\frac{1}{2}$个单位长度 | D． | 向右平移$\frac{π}{6}$个单位长度 |
双流中学食堂旁边有一块矩形空地，学校想要在这块空地上修建一个内接四边形EFGH花坛（如图所示），该花坛的四个顶点分别落在矩形的四条边上，已知AB=a（a＞10），BC=10，且 AE=AH=CG=CF，设AE=x，花坛EFGH的面积记为S（x）．