(1)已知p3+q3=2.求证p+q≤2.用反证法证明时.可假设p+q≥2.(2)已知a.b∈R.|a|+|b|＜1.求证方程x2+ax+b=0的两根的绝对值都小于1．用反证法证明时可假设方程至少有一根的绝对值大于或等于1．以下结论正确的是( )A．的假设都错误B．的假设都正确C．的假设正确D．的假设错误题目和参考答案——青夏教育精英家教网——

题目内容

16．（1）已知p³+q³=2，求证p+q≤2，用反证法证明时，可假设p+q≥2，
（2）已知a，b∈R，|a|+|b|＜1，求证方程x²+ax+b=0的两根的绝对值都小于1．
用反证法证明时可假设方程至少有一根的绝对值大于或等于1．以下结论正确的是（　　）

	A．	（1）与（2）的假设都错误		B．	（1）与（2）的假设都正确
	C．	（1）的假设错误；（2）的假设正确		D．	（1）的假设正确；（2）的假设错误

分析利用反证法的定义进行分析求解．

解答解：（1）用反证法证明时，假设命题为假，应为全面否定．
所以p+q≤2的假命题应为p+q＞2．故（1）错误；
（2）已知a，b∈R，|a|+|b|＜1，求证方程x²+ax+b=0的两根的绝对值都小于1，
根据反证法的定义，可假设|x₁|≥1，故（2）正确；
故选：C．

点评此题主要考查反证法的定义及其应用，是一道基础题．

练习册系列答案

中考数学合成演练30天系列答案

汇测期末竞优系列答案

素质提优123系列答案

随堂练123系列答案

随堂新卷系列答案

堂堂清课堂8分钟小测系列答案

特级教师小学毕业升学系统总复习系列答案

提分计划单元期末系列答案

经纶学典提优作业本系列答案

题粹系列答案

相关题目

6．已知椭圆M：x²+2y²=2．
（Ⅰ）求椭圆M的离心率；
（Ⅱ）设O为坐标原点，A，B，C为椭圆M上的三个动点，若四边形OABC为平行四边形，判断△ABC的面积是否为定值，并说明理由．

7．用反证法证明命题“设a，b是实数，则方程x³+ax+b=0至少有一个实根”时，要做的反设是（4）（填序号）
（1）方程x³+ax+b=0恰好有两个实根（2）方程x³+ax+b=0至多有一个实根
（3）方程x³+ax+b=0至多有两个实根（4）方程x³+ax+b=0没有实根．

4．某商场柜台销售某种产品，每件产品的成本为10元，并且每件产品需向该商场交a元（3≤a≤7）的管理费，预计当每件产品的售价为x元（20≤x≤25）时，一天的销售量为（x-30）²件．
（Ⅰ）求该柜台一天的利润f（x）（元）与每件产品的售价x的函数关系式；
（Ⅱ）当每件产品的售价为多少元时，该柜台一天的利润f（x）最大，并求出f（x）的最大值g（a）．

11．设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左焦点为F₁，右焦点F₂，直线l₁过点F₁且垂直于椭圆的长轴，动直线l₂垂直l₁于点P，线段PF₂垂直平分线交l₂于点M．
（1）求点M的轨迹E的方程；
（2）若点A的坐标为（2，4），直线l：x=ky+2（k∈R），与曲线E相交于B，C两点，直线AB，AC分别交直线l₁于点S、T，试判断以线段ST为直径的圆是否恒过两个定点？若是，求这两个定点的坐标；若不是，说明理由．

已知函数f（x）=cos（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象，如图所示．
（1）求函数解析式，并求出函数的单调增区间；
（2）若方程f（x）=m在[-$\frac{π}{6}$，$\frac{13π}{12}$]有两个不同的实根，求m的取值范围．

8．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{x}-1，x＞0}\\{{x}^{2}+1，x≤0}\end{array}\right.$，若存在x₁∈（0，+∞），x₂∈（-∞，0]，使得f（x₁）=f（x₂），则x₁的最小值为（　　）

如图，将抛物线C₁：y=$\frac{1}{2}$x²+2x沿x轴对称后，向右平移3个单位，再向下平移5个单位，得到抛物线C₂，若抛物线C₁的顶点为A，点P是抛物线C₂上一点，则△POA的面积的最小值为（　　）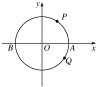

如图，动点P，Q从点A（3，0）出发绕⊙O作圆周运动，若点M按逆时针方向每秒钟转$\frac{π}{3}$rad，点N按顺时针方向每秒钟转$\frac{π}{6}$rad．则当M、N第一次相遇时，点M转过的弧长为4π．