Question

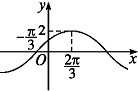
若函数f（x）=2sin（ωx+φ）的部分图象如图所示，则ω和φ的取值是（　　）

• A、ω=

  1

  2

  ，φ=-

  π

  6

• B、ω=

  1

  2

  ，φ=

  π

  6

• C、ω=1，φ=-

  π

  3

• D、ω=1，φ=

  π

  3

Answer 1

考点：正弦函数的图象

专题：三角函数的图像与性质

分析：根据函数的图象，即可得到结论．

解答： 解：由图象可知

T

4

=

2π

3

-(-

π

3

)=π，
则函数的周期T=4π=

2π

ω

，
∴ω=

1

2

，
此时f（x）=2sin（

1

2

x+φ），
∵当x=

2π

3

时，y=2，
∴

2π

3

×

1

2

+φ=

π

2

，
解得φ=

π

6

，
故ω=

1

2

，φ=

π

6

，
故选：B

点评：本题主要考查三角函数解析式的求解，根据函数周期性以及函数过定点建立条件关系是解决本题的关键．