题目内容
当x∈(0,
)时,下面四个函数中最大的是( )
| π |
| 4 |
| A、sin(cosx) |
| B、sin(sinx) |
| C、cos(sinx) |
| D、cos(cosx) |
考点:三角函数线
专题:计算题,三角函数的求值
分析:由x∈(0,
),可得0<sinx<cosx<
,利用y=sinx在(0,
)上单调递增,y=cosx在(0,
)上单调递减,即可得出结论.
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:∵x∈(0,
),
∴0<sinx<cosx<
<
,
∵y=sinx在(0,
)上单调递增,∴sin(sinx)<sin(cosx),
y=cosx在(0,
)上单调递减,∴cos(sinx)>cos(sinx),
∵sin(cosx)<cos(sinx),
∴cos(sinx)最大.
故选:C.
| π |
| 4 |
∴0<sinx<cosx<
| ||
| 2 |
| π |
| 2 |
∵y=sinx在(0,
| ||
| 2 |
y=cosx在(0,
| ||
| 2 |
∵sin(cosx)<cos(sinx),
∴cos(sinx)最大.
故选:C.
点评:本题考查三角函数的单调性,考查学生的计算能力,比较基础.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
| 1+2i |
| 1+i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
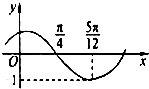 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|
在△ABC中,tanA=
,cosB=
,则sinC=( )
| 1 |
| 2 |
3
| ||
| 10 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、-2 |
若0<x<
,则xtanx>1是xsinx>1的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)=
,则f(π)-f(3.14)等于( )
|
| A、0 | B、2 | C、-2 | D、±2 |
已知函数f(x)=x3+
(x∈R),f(x1)+f(x2)>0,则下列不等式中正确的是( )
| 2x-1 |
| 2x+1 |
| A、x1>x2 |
| B、x1<x2 |
| C、x1+x2>0 |
| D、x1+x2<0 |