题目内容
绘制函数f（x）=x2+2|x|的图象（不用写作法），并依据图象求出函数的增区间和函数的值域．
考点：函数的图象
专题：作图题
分析：∵f（-x）--f（x），∴f（x）为偶函数，所以只要画出x∈（0，+∞）的图象，关于y轴对称可得x∈（-∞，0）的图象．特别地，x＞0时，图象为抛物线的一部分．
解答：
解：函数f（x）=x2+2|x|的图象：
从图可得知函数的递增区间为（0，+∞），
值域为：[0，+∞）
从图可得知函数的递增区间为（0，+∞），
值域为：[0，+∞）
点评：画函数的图象，要从函数的性质入手，利用对称性；当有绝对值时，要想法去掉．
练习册系列答案
相关题目
集合A={x|-1≤2x+1≤3}，B={x|x（x-2）≤0}，则A∩B=（ ）
| A、{x|-1≤x＜0} |
| B、{x|0＜x≤1} |
| C、{x|0≤x≤2} |
| D、{x|0≤x≤1} |
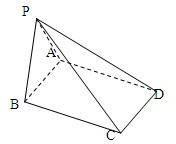如图，四棱锥P-ABCD的底面是AB=2，BC=