题目内容
已知曲线C的方程为y2=4x,过原点作斜率为1的直线和曲线C相交,另一个交点记为P1,过P1作斜率为2的直线与曲线C相交,另一个交点记为P2,过P2作斜率为4的直线与曲线C相交,另一个交点记为P3,…,如此下去,一般地,过点Pn作斜率为2n的直线与曲线C相交,另一个交点记为Pn+1,设点Pn(xn,yn)(n∈N*).
(1)指出y1,并求yn+1与yn的关系式(n∈N*);
(2)求{y2n-1}(n∈N*)的通项公式,并指出点列P1,P3,…,P2n+1,…向哪一点无限接近?说明理由;
(3)令an=y2n+1-y2n-1,数列{an}的前n项和为Sn,设bn=
,求所有可能的乘积bi•bj(1≤i≤j≤n)的和.
(1)指出y1,并求yn+1与yn的关系式(n∈N*);
(2)求{y2n-1}(n∈N*)的通项公式,并指出点列P1,P3,…,P2n+1,…向哪一点无限接近?说明理由;
(3)令an=y2n+1-y2n-1,数列{an}的前n项和为Sn,设bn=
| 1 | ||
|
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)利用曲线的相交关系,联立方程组求解;
(2)由(1)得出y2n-1-y2n-3=-(
)n-2 (n≥2),利用累加法求通项公式;
(3)借助矩阵研究并所有可能的乘积bi•bj(1≤i≤j≤n)的和.
(2)由(1)得出y2n-1-y2n-3=-(
| 1 |
| 4 |
(3)借助矩阵研究并所有可能的乘积bi•bj(1≤i≤j≤n)的和.
解答:
解:(1)y1=4---------------1分
设Pn(xn,yn),Pn+1(xn+1,yn+1),由题意得
,----------------2分
解得yn+1+yn=4•(
)n.------------------------------------------------4分
(2)分别用2n-3、2n-2代换上式中的n得
⇒y2n-1-y2n-3=-2•(
)2n-3=-(
)n-2 (n≥2)------------------------6分
又y1=4,y2n-1=
+
(
)n-1(n∈N*),----------------------------------8分
∵
y2n-1=
,∴点列P1,P3,…,P2n+1,…向点(
,
)无限接近-------10分
(3)∵an=y2n+1-y2n-1=-(
)n-1,∴Sn=-
•[1-(
)n],-------------------11分
bn=4n,bibj=4i+j (1≤i≤j≤n).--------------------------------12分
将所得的积排成如下矩阵:
A=
,设矩阵A的各项和为S.
在矩阵的左下方补上相应的数可得B=
,
矩阵B中第一行的各数和S1=42+43+…+4n+1=
(4n-1),
矩阵B中第二行的各数和S2=43+44+…+4n+2=
(4n-1),
…
矩阵B中第N行的各数和Sn=4n+1+4n+2+…+4n+n=
(4n-1),--------15分
从而矩阵B中的所有数之和为S1+S2+…+Sn=
(4n-1)---------------16分
所有可能的乘积bi•bj(1≤i≤j≤n)的和
S=
[
(4n-1)2-(42+44+…+42n)]+(42+44+…+42n)
=
.-----------------------------------------18分
设Pn(xn,yn),Pn+1(xn+1,yn+1),由题意得
|
解得yn+1+yn=4•(
| 1 |
| 2 |
(2)分别用2n-3、2n-2代换上式中的n得
|
⇒y2n-1-y2n-3=-2•(
| 1 |
| 2 |
| 1 |
| 4 |
又y1=4,y2n-1=
| 8 |
| 3 |
| 4 |
| 3 |
| 1 |
| 4 |
∵
| lim |
| n→∞ |
| 8 |
| 3 |
| 16 |
| 9 |
| 8 |
| 3 |
(3)∵an=y2n+1-y2n-1=-(
| 1 |
| 4 |
| 4 |
| 3 |
| 1 |
| 4 |
bn=4n,bibj=4i+j (1≤i≤j≤n).--------------------------------12分
将所得的积排成如下矩阵:
A=
|
在矩阵的左下方补上相应的数可得B=
|
矩阵B中第一行的各数和S1=42+43+…+4n+1=
| 16 |
| 3 |
矩阵B中第二行的各数和S2=43+44+…+4n+2=
| 64 |
| 3 |
…
矩阵B中第N行的各数和Sn=4n+1+4n+2+…+4n+n=
| 4n+1 |
| 3 |
从而矩阵B中的所有数之和为S1+S2+…+Sn=
| 16 |
| 9 |
所有可能的乘积bi•bj(1≤i≤j≤n)的和
S=
| 1 |
| 2 |
| 16 |
| 9 |
=
| 42n+3-5•4n+2+16 |
| 45 |
点评:考查直线与曲线的交点问题的处理方法,以及数列求和的方法,借助矩阵研究数列问题的方法.

练习册系列答案
相关题目
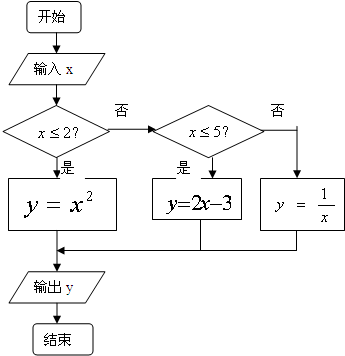 如图:
如图: