题目内容
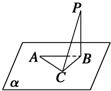如图，定点A和B都在平面α内，定点P∉α，PB⊥α，C是平面α内异于A和B的动点，且PC⊥AC，则△ABC为（ ）| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：通过证明AC⊥平面PBC，得出AC⊥BC，即可得出△ABC是直角三角形．
解答：
解：△ABC是直角三角形，说明如下；
∵A∈α，C∈α，∴AC?α；
又∵PB⊥α，∴PB⊥AC；
又∵PC⊥AC，
PB∩PC=B，
∴AC⊥平面PBC；
又∵BC?平面PBC，
∴AC⊥BC；
∴△ABC是直角三角形．
故选：A．
∵A∈α，C∈α，∴AC?α；
又∵PB⊥α，∴PB⊥AC；
又∵PC⊥AC，
PB∩PC=B，
∴AC⊥平面PBC；
又∵BC?平面PBC，
∴AC⊥BC；
∴△ABC是直角三角形．
故选：A．
点评：本题考查了空间中的垂直关系的判断问题，解题时应明确线线垂直和线面垂直的判断与性质是什么，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列计算不正确的是（ ）
| A、log3243=log335=5log33=5×1=5 | ||||
B、log510-log52=log5
| ||||
| C、lg2+lg5=lg（2×5）=lg10=1 | ||||
D、log8（8×4）=log88+log84=1+
|
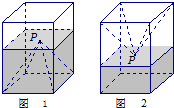如图1，一个正四棱柱形（底面是正方形）的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块（内部不渗水），容器内盛有a升水时，水面恰好经过正四棱锥的顶点P．如果将容器倒置，水面也恰好过点P（图2）．有下列四个命题：