题目内容
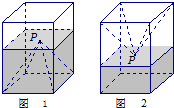 如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:
如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:①正四棱锥的高等于正四棱柱高的一半;
②将容器侧面水平放置时,水面也恰好过点P;
③任意摆放该容器,当水面静止时,水面都恰好经过点P;
④若往容器内再注入a升水,则容器恰好能装满.
其中真命题的代号是:( )(写出所有正确命题的代号).
| A、②和③ | B、①和② |
| C、②和④ | D、③和④ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:设图(1)水的高度h2,几何体正四棱柱的高为h1,底面正方形的边长为b,图(2)中水的体积为b2h1-b2h2=b2(h1-h2),
对于①,易知
b2h2=b2(h1-h2),所以h1=
h2,故①错误,D正确;
②对于②,当容器侧面水平放置时,P点在长方体中截面上,又水占容器内空间的一半,所以水面也恰好经过P点,故B正确.
③对于③,假设③正确,当水面与正四棱锥的一个侧面重合时,经计算得水的体积为
b2h2>
b2h2,导出矛盾,从而可得答案.
对于①,易知
| 2 |
| 3 |
| 5 |
| 3 |
②对于②,当容器侧面水平放置时,P点在长方体中截面上,又水占容器内空间的一半,所以水面也恰好经过P点,故B正确.
③对于③,假设③正确,当水面与正四棱锥的一个侧面重合时,经计算得水的体积为
| 25 |
| 36 |
| 2 |
| 3 |
解答:
解:设图(1)水的高度h2,几何体正四棱柱的高为h1,底面正方形的边长为b,
图(2)中水的体积为b2h1-b2h2=b2(h1-h2),
所以b2h2-
b2h2=
b2h2=b2(h1-h2),所以h1=
h2,故①错误,D正确.
对于②,当容器侧面水平放置时,P点在长方体中截面上,
又水占容器内空间的一半,所以水面也恰好经过P点,故B正确.
对于③,假设③正确,当水面与正四棱锥的一个侧面重合时,
经计算得水的体积为
b2h2>
b2h2,矛盾,故③不正确.
综上所述,正确的是②④,
故选:C.
图(2)中水的体积为b2h1-b2h2=b2(h1-h2),
所以b2h2-
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
对于②,当容器侧面水平放置时,P点在长方体中截面上,
又水占容器内空间的一半,所以水面也恰好经过P点,故B正确.
对于③,假设③正确,当水面与正四棱锥的一个侧面重合时,
经计算得水的体积为
| 25 |
| 36 |
| 2 |
| 3 |
综上所述,正确的是②④,
故选:C.
点评:本题主要考查对柱、锥、台、球的结构特征等考点的理解,考查空间思维与运算能力,属于难题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知集合A={x∈N|0<x<3},B={x|2x-1>1},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
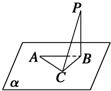 如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )
如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |