题目内容
在△ABC中，a、b、c分别为内角A、B、C的对边，若b=2asinB，求∠A的度数．
考点：余弦定理
专题：计算题,解三角形
分析：已知等式利用正弦定理化简，根据sinB不为0，求出sinA的值，讨论A为锐角和钝角，利用特殊角的三角函数值即可求出A的度数．
解答：
解：∵b=2asinB，
∴由正弦定理化简得：sinB=2sinAsinB，
∵sinB≠0，
∴sinA=
，
∵0＜A＜π，
∴A=30°或150°．
∴由正弦定理化简得：sinB=2sinAsinB，
∵sinB≠0，
∴sinA=
| 1 |
| 2 |
∵0＜A＜π，
∴A=30°或150°．
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
设a=1.70.7，b=0.71.2，c=log0.71.2，则a、b、c的大小关系是（ ）
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜a＜c |
| D、c＜b＜a |
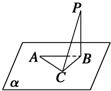如图，定点A和B都在平面α内，定点P∉α，PB⊥α，C是平面α内异于A和B的动点，且PC⊥AC，则△ABC为（ ）| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
下列哪一组函数相等（ ）
A、f（x）=x与g（x）=
| |||
B、f(x)=x2与g(x)=(
| |||
C、f(x)=|x|与g(x)=(
| |||
D、f（x）=x2与g（x）=
|