题目内容
已知抛物线y2=4x的准线与x轴的交点为A,焦点为F,l是过点A且倾斜角为
的直线,则点F到直线l的距离等于( )
| π |
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:直线与圆锥曲线的关系
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,A(-1,0),F(1,0),求出过点A且倾斜角为
的直线l的方程,再利用点到直线的距离公式,即可求出点F到直线l的距离.
| π |
| 3 |
解答:
解:由题意,A(-1,0),F(1,0),则
过点A且倾斜角为
的直线l的方程为y=
(x+1),即
x-y+
=0,
∴点F到直线l的距离=
=
,
故选:B.
过点A且倾斜角为
| π |
| 3 |
| 3 |
| 3 |
| 3 |
∴点F到直线l的距离=
2
| ||
|
| 3 |
故选:B.
点评:本题考查抛物线的性质,考查点F到直线l的距离,确定直线的方程是关键.

练习册系列答案
相关题目
已知集合A={x∈N|0<x<3},B={x|2x-1>1},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
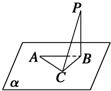 如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )
如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
函数f(x)=2|log2x|+1的图象大致是( )
A、 |
B、 |
C、 |
D、 |
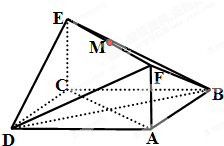 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=