题目内容
已知两个不同集合A={1，3，a2-a+3}，B={1，5，a2+2a}，A∩B={1，3}，求a的值及集合A．
考点：交集及其运算
专题：集合
分析：由A∩B={1，3}得：a2+2a=3，解之得a=1，或a=-3．然后对a分类讨论得答案．
解答：
解：由A∩B={1，3}得：a2+2a=3，解之得a=1，或a=-3．
（1）当a=1时，a2-a+3=3，A={1，3，3}与集合中元素的互异性矛盾，所以a≠1．
（2）当a=-3时，a2-a+3=15，A={1，3，15}，A∩B={1，3}与题意相符．
∴a=-3，此时，A={1，3，15}．
（1）当a=1时，a2-a+3=3，A={1，3，3}与集合中元素的互异性矛盾，所以a≠1．
（2）当a=-3时，a2-a+3=15，A={1，3，15}，A∩B={1，3}与题意相符．
∴a=-3，此时，A={1，3，15}．
点评：本题考查了交集及其运算，体现了分类讨论的数学思想方法，是基础题．
练习册系列答案
相关题目
设a=1.70.7，b=0.71.2，c=log0.71.2，则a、b、c的大小关系是（ ）
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜a＜c |
| D、c＜b＜a |
已知集合A={x∈N|0＜x＜3}，B={x|2x-1＞1}，则A∩B=（ ）
| A、∅ | B、{1} |
| C、{2} | D、{1，2} |
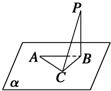如图，定点A和B都在平面α内，定点P∉α，PB⊥α，C是平面α内异于A和B的动点，且PC⊥AC，则△ABC为（ ）| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |