题目内容
若不等式
≥|a2-a|对x∈(1,2]恒成立,则实数a的取值范围为 .
| 2 |
| x-1 |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:由x的取值范围求得
≥2,把不等式
≥|a2-a|对x∈(1,2]恒成立转化为-2≤a2-a≤2恒成立,然后求解不等式组得答案.
| 2 |
| x-1 |
| 2 |
| x-1 |
解答:
解:∵x∈(1,2],
∴0<x-1≤1.
≥2.
∴要使不等式
≥|a2-a|对x∈(1,2]恒成立,
即|a2-a|≤2恒成立,
也就是-2≤a2-a≤2恒成立.
即
,解得-1≤a≤2.
∴实数a的取值范围为[-1,2].
故答案为:[-1,2].
∴0<x-1≤1.
| 2 |
| x-1 |
∴要使不等式
| 2 |
| x-1 |
即|a2-a|≤2恒成立,
也就是-2≤a2-a≤2恒成立.
即
|
∴实数a的取值范围为[-1,2].
故答案为:[-1,2].
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,考查了不等式组的解法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
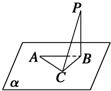 如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )
如图,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为( )| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
函数f(x)=2|log2x|+1的图象大致是( )
A、 |
B、 |
C、 |
D、 |
下列哪一组函数相等( )
A、f(x)=x与g(x)=
| |||
B、f(x)=x2与g(x)=(
| |||
C、f(x)=|x|与g(x)=(
| |||
D、f(x)=x2与g(x)=
|