Question

已知函数f(x)=ax²+bx+1(a,b为常数),x∈R,

F(x)=

(1)若f(-1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;

(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;

(3)设m·n<0,m+n>0,a>0且f(x)为偶函数,证明F(m)+F(n)>0.

Answer 1

 (1)解:∵f(-1)=0,

∴a-b+1=0,a=b-1.

又x∈R,f(x)的值域为[0,+∞),

∴

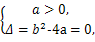
∴b²-4(b-1)=0,b=2,a=1,

∴f(x)=x²+2x+1=(x+1)².

∴F(x)=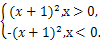

(2)解:g(x)=f(x)-kx

=x²+2x+1-kx

=x²+(2-k)x+1,

当≥2或≤-2时,

即k≥6或k≤-2时,g(x)在[-2,2]上是单调函数.

故所求实数k的取值范围为(-∞,-2]∪[6,+∞).

(3)证明:∵f(x)是偶函数,

∴f(x)=ax²+1,F(x)=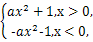

∵m·n<0,不妨设m>n,

则n<0,

又m+n>0,m>-n>0,

∴m²>n²,

又a>0,

∴F(m)+F(n)=(am²+1)-an²-1

=a(m²-n²)>0.

命题得证.