题目内容
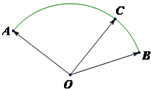如图，半径为| 3 |
 |
| AB |
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，建立直角坐标系．由∠BOC=30°，OC=
．可得C（
cos30°，
sin30°）．由∠BOA=120°，可得A（
cos120°，
sin120°）．又B（
，0），
=λ
+μ
，利用向量相等即可得出λ，μ．
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| OC |
| OA |
| OB |
解答：
解：如图所示，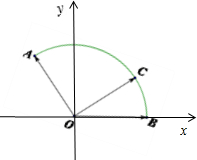
建立直角坐标系．
∵∠BOC=30°，OC=
．
∴C（
cos30°，
sin30°），
即C（
，
）．
∵∠BOA=120°，
∴A（
cos120°，
sin120°），
即A（-
，
）．
又B（
，0），
=λ
+μ
，
∴（
，
）=λ（-
，
）+μ（
，0）．
∴
，解得
．
∴λ+μ=
．
故答案为：
建立直角坐标系．
∵∠BOC=30°，OC=
| 3 |
∴C（
| 3 |
| 3 |
即C（
| 3 |
| 2 |
| ||
| 2 |
∵∠BOA=120°，
∴A（
| 3 |
| 3 |
即A（-
| ||
| 2 |
| 3 |
| 2 |
又B（
| 3 |
| OC |
| OA |
| OB |
∴（
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴
|
|
∴λ+μ=
| 3 |
故答案为：
| 3 |
点评：本题考查了向量的坐标运算和向量相等，属于中档题．
练习册系列答案
相关题目
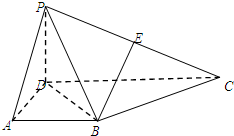在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．