题目内容
已知椭圆C:
+
=1(a>b>0)过点(2,0),且椭圆C的离心率为
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线x=-1上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线l⊥MN.证明:直线l恒过定点,并求出该定点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线x=-1上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线l⊥MN.证明:直线l恒过定点,并求出该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)点(2,0)在椭圆上,将其代入椭圆方程,又因为c=
,解方程组得到a,b,由此能求出椭圆方程.
(Ⅱ)点P在直线x=-1上,则可得P(-1,y2),当直线MN的斜率存在时设斜率为k,得到直线MN中点,根据点P的横坐标解得k,由l⊥MN可得直线l的斜率及其含参数y3的方程,分析得直线是否恒过定点,注意还要讨论直线MN的斜率不存在的情况.
| 1 |
| 2 |
(Ⅱ)点P在直线x=-1上,则可得P(-1,y2),当直线MN的斜率存在时设斜率为k,得到直线MN中点,根据点P的横坐标解得k,由l⊥MN可得直线l的斜率及其含参数y3的方程,分析得直线是否恒过定点,注意还要讨论直线MN的斜率不存在的情况.
解答:
(Ⅰ)解:∵点(2,0)在椭圆上,
∴
+
=1,解得a2=4,
∵椭圆C的离心率为
,∴
=
,
∴
=
,解得b2=3,
∴椭圆C的方程为
+
=1.
(Ⅱ)证明:设P(-1,y0),y0∈(-
,
),
①当直线MN的斜率存在时,
设直线MN的方程为y-y0=k(x+1),M(x1,y1),N(x2 ,y2),
由
,
得:(3+4k2)x2+(8ky0+8k2)x+(4y02+8ky0+4k2-12)=0,
∴x1+x2=-
,
∵P为MN中点,∴
=-1,即-
=-2,
∴kMN=
(y0≠0).
∵l⊥⊥MN,∴kl=-
,
∴直线l的方程为y-y0=-
(x+1),
即y=-
(x+
),
∴直线l恒过定点(-
,0).
②当直线MN的斜率不存在时,
直线MN的方程为x=-1,
此时直线l为x轴,也过点(-
,0).
综上所述,直线l恒过定点(-
,0).
∴
| 4 |
| a2 |
| 0 |
| b2 |
∵椭圆C的离心率为
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∴
| a2-b2 |
| a2 |
| 1 |
| 4 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:设P(-1,y0),y0∈(-
| 3 |
| 2 |
| 3 |
| 2 |
①当直线MN的斜率存在时,
设直线MN的方程为y-y0=k(x+1),M(x1,y1),N(x2 ,y2),
由
|
得:(3+4k2)x2+(8ky0+8k2)x+(4y02+8ky0+4k2-12)=0,
∴x1+x2=-
| 8ky0+8k2 |
| 3+4k2 |
∵P为MN中点,∴
| x1+x2 |
| 2 |
| 8ky0+8k2 |
| 3+4k2 |
∴kMN=
| 3 |
| 4y0 |
∵l⊥⊥MN,∴kl=-
| 4y0 |
| 3 |
∴直线l的方程为y-y0=-
| 4y0 |
| 3 |
即y=-
| 4y0 |
| 3 |
| 1 |
| 4 |
∴直线l恒过定点(-
| 1 |
| 4 |
②当直线MN的斜率不存在时,
直线MN的方程为x=-1,
此时直线l为x轴,也过点(-
| 1 |
| 4 |
综上所述,直线l恒过定点(-
| 1 |
| 4 |
点评:本题考查椭圆方程的求法,考查直线恒过定点的证明,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
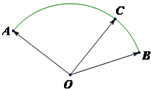 如图,半径为
如图,半径为
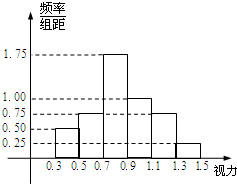 从某校高三年级随机抽取一个班,对该班45名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班45名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为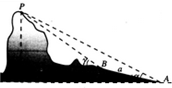 如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=
如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=