题目内容
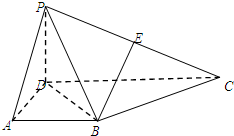 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.(1)求证:BE∥平面PAD;
(2)求证:BC⊥平面PBD;
(3)已知在侧棱PC上存在一点Q,使得二面角Q-BD-P为45°,求
| PQ |
| PC |
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)根据线面平行的判定定理即可证明BE∥平面PAD;
(2)根据线面垂直的判定定理即可证明BC⊥平面PBD;
(3)建立空间直角坐标系,求出向量的法向量,根据向量法与二面角之间的关系,即可求出
.
(2)根据线面垂直的判定定理即可证明BC⊥平面PBD;
(3)建立空间直角坐标系,求出向量的法向量,根据向量法与二面角之间的关系,即可求出
| PQ |
| PC |
解答:
 解:(1)取PD的中点F,连结EF,AF,
解:(1)取PD的中点F,连结EF,AF,
因为E为PC中点,所以EF∥CD,
且EF=
CD=1,在梯形ABCD中,AB∥CD,AB=1,
所以EF∥AB,EF=AB,四边形ABEF为平行四边形,所以BE∥AF,
BE?平面PAD,AF?平面PAD,
所以BE∥平面PAD.
(2)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
所以PD⊥AD.如图,以D为原点建立空间直角坐标系D-xyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1),
=(1,1,0),
=(-1,1,0).
所以
•
=0,BC⊥DB,
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.
(3)平面PBD的法向量为
=(-1,1,0),
=(0,2,-1),
=λ
,λ∈(0,1),
所以
=(0,2λ,-λ),
设平面QBD的法向量为
=(a,b,c),f′(x)=0,得x1=
,x2=
,
由
•
=0,
•
=0,
所以
所以
=(-1,1,
),…(10分)
所以cos45°=
=
=
,
注意到λ∈(0,1),得λ=
-1.所以
=
-1.
 解:(1)取PD的中点F,连结EF,AF,
解:(1)取PD的中点F,连结EF,AF,因为E为PC中点,所以EF∥CD,
且EF=
| 1 |
| 2 |
所以EF∥AB,EF=AB,四边形ABEF为平行四边形,所以BE∥AF,
BE?平面PAD,AF?平面PAD,
所以BE∥平面PAD.
(2)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
所以PD⊥AD.如图,以D为原点建立空间直角坐标系D-xyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1),
| DB |
| BC |
所以
| BC |
| DB |
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.
(3)平面PBD的法向量为
| BC |
| PC |
| PQ |
| PC |
所以
| PQ |
设平面QBD的法向量为
| n |
-a-
| ||
| 2 |
-a+
| ||
| 2 |
由
| n |
| DB |
| n |
| DQ |
所以
|
所以
| n |
| 2λ |
| λ-1 |
所以cos45°=
n•
| ||
|n||
|
| 2 | ||||||
|
| ||
| 2 |
注意到λ∈(0,1),得λ=
| 2 |
| PQ |
| PC |
| 2 |
点评:本题主要考查空间直线和平面,平行和垂直的判定,以及空间二面角的求解,要求熟练掌握相应的判定定理以及,空间向量与二面角的关系.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
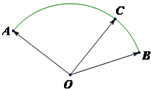 如图,半径为
如图,半径为
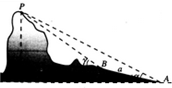 如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=
如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角β=15°的斜坡向上走100米到B,在B处测得山顶P的仰角为γ=60°,则山高h=