题目内容
已知点P（x，y）是椭圆
+
=1上的一个动点，则点P到直线2x+y-10=0的距离的最小值为 ．
| x2 |
| 4 |
| y2 |
| 9 |
考点：直线与圆锥曲线的关系,两条平行直线间的距离
专题：计算题,圆锥曲线的定义、性质与方程
分析：设与直线2x+y-10=0平行的直线方程为：2x+y+c=0，与椭圆方程联立，消元，令△=0，可得c的值，求出两条平行线间的距离，即可求得椭圆
+
=1上一点P到直线2x+y-10=0的距离最小值．
| x2 |
| 4 |
| y2 |
| 9 |
解答：
解：设与直线2x+y-10=0平行的直线方程为：2x+y+c=0，
与椭圆方程联立，消元可得25x2+16cx+4c2-36=0
令△=256c2-100（4c2-36）=0，可得c=±5．
∴两条平行线间的距离为
=3
或
．
∴点P到直线2x+y-10=0的距离的最小值为
．
故答案为：
．
与椭圆方程联立，消元可得25x2+16cx+4c2-36=0
令△=256c2-100（4c2-36）=0，可得c=±5．
∴两条平行线间的距离为
| |±5-10| | ||
|
| 5 |
| 5 |
∴点P到直线2x+y-10=0的距离的最小值为
| 5 |
故答案为：
| 5 |
点评：本题考查直线与椭圆的位置关系，解题的关键是求出与直线2x+y-10=0平行，且与椭圆相切的直线方程．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
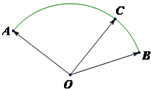如图，半径为
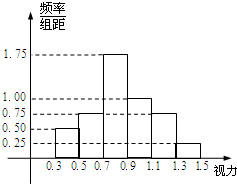从某校高三年级随机抽取一个班，对该班45名学生的高校招生体检表中视力情况进行统计，其结果的频率分布直方图如图．若某高校A专业对视力的要求在0.9以上，则该班学生中能报A专业的人数为