题目内容
已知向量
=2
-3
，
=4
-2
，
=3
+
，将向量
用向量
，
表示为 ．
| m |
| a |
| b |
| n |
| a |
| b |
| p |
| a |
| b |
| p |
| m |
| n |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用向量的运算和数乘运算即可得出．
解答：
解：∵向量
=2
-3
，
=4
-2
，
∴
=-
+
，
=
-
．
∴
=3(-
+
)+(
-
)=-
+
．
故答案为：
=-
+
．
| m |
| a |
| b |
| n |
| a |
| b |
∴
| a |
| 1 |
| 4 |
| m |
| 3 |
| 8 |
| n |
| b |
| 1 |
| 4 |
| n |
| 1 |
| 2 |
| m |
∴
| p |
| 1 |
| 4 |
| m |
| 3 |
| 8 |
| n |
| 1 |
| 4 |
| n |
| 1 |
| 2 |
| m |
| 5 |
| 4 |
| m |
| 11 |
| 8 |
| n |
故答案为：
| p |
| 5 |
| 4 |
| m |
| 11 |
| 8 |
| n |
点评：本题考查了向量的线性运算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
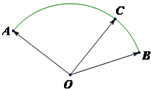如图，半径为