题目内容
11.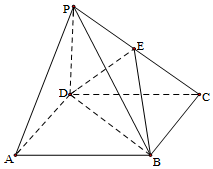 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.(1)证明PA∥面EDB;
(2)求异面直线PC与AD能成角的大小.
分析 (1)连接AC交BD于O,连接OE,证明OE∥PA,即可证明PA∥平面EDB;
(2)证明AD⊥平面PCD,即可证明AD⊥PC,可得异面直线PC与AD所成角的大小.
解答 证明:(1)连接AC交BD于O,连接OE
∵底面ABCD是正方形,∴O为AC中点,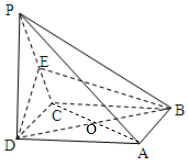
∵在△PAC中,E是PC的中点,
∴OE∥PA,…(3分)
∵OE?平面EDB,PA?平面EDB,
∴PA∥平面EDB.…(5分)
(2)∵侧棱PD⊥底面ABCD,AD?底面ABCD,
∴PD⊥AD,
∵底面ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,
∴AD⊥平面PCD.…(8分)
∴AD⊥PC,
∴异面直线PC与AD所成角为90°.…(12分)
点评 本题考查线面平行、垂直的证明,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定定理是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为$\sqrt{3}$,则此球的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
2.在平面直角坐标系中,已知三点A(1,-2),B(2,-1),C(0,-2),则|$\overrightarrow{AB}$+$\overrightarrow{BC}$|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是( )
| A. | (-∞,5) | B. | (-∞,5] | C. | (5,+∞) | D. | [5,+∞) |
6.“a>b”是“2a>2b”的_________条件.( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
20.若“0<x<1”是“(x-a)[x-(a+2)]<0”的充分不必要条件,则实数a的取值范围是( )
| A. | [-1,0] | B. | (-1,0) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,-1)∪(0,+∞) |