题目内容
16.求以原点为顶点,坐标轴为对称轴,并且经过点(6,4)的抛物线的标准方程.分析 根据题意,分析可得要求抛物线开口向上或向右,则设其标准方程为y2=2p1x(p1>0)①或x2=2p2y(p2>0)②,将点的坐标代入标准方程,计算可得p1、p2的值,即可得答案.
解答 解:根据题意,抛物线过点(6,4),则开口向上或向右,
则设其标准方程为y2=2p1x(p1>0)①或x2=2p2y(p2>0)②,
将点(6,4)代入①可得:
16=12p1,解可得p1=$\frac{4}{3}$,
即其方程为y2=$\frac{8}{3}$x;
将点(6,4)代入②可得:
36=8p2,解可得p2=$\frac{9}{2}$,
即其方程为x2=9y;
故所求抛物线方程为y2=$\frac{8}{3}$x或x2=9y.
点评 本题考查抛物线的标准方程,注意由抛物线过点的坐标设出抛物线的方程.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<0}\\{|\frac{1}{2}{x}^{2}-2x+1|,x≥0}\end{array}\right.$,方程f2(x)-af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
| A. | [6,11] | B. | [3,11] | C. | (6,11) | D. | (3,11) |
1.对于R上可导函数f(x),若满足(x-2)f′(x)>0,则必有( )
| A. | f(1)+f(3)<2f(2) | B. | f(1)+f(3)>2f(2) | C. | f(1)+f(3)>f(0)+f(4) | D. | f(1)+f(0)<f(3)+f(4) |
8.已知y=$\frac{1}{3}{x^3}+b{x^2}$+(b+2)x+3是R上的单调函数,则b的取值范围是( )
| A. | -1≤b≤2 | B. | b≤-1或b≥2 | C. | -1<b<2 | D. | b<-1或b>2 |
5.已知x,y都是实数,命题p:|x|<3;命题q:x2-2x-3<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |

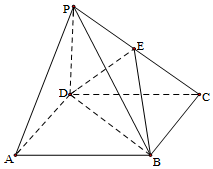 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.