题目内容
3.设曲线C的参数方程为$\left\{\begin{array}{l}x=2+3cosθ\\ y=1+3sinθ\end{array}\right.$(θ为参数),直线l的方程为x-3y+2=0,则曲线C上到直线l的距离为$\frac{{7\sqrt{10}}}{10}$的点的个数为4个.分析 由题意将圆C和直线l先化为一般方程坐标,然后再计算曲线C上到直线l距离为$\frac{{7\sqrt{10}}}{10}$的点的个数.
解答 解:化曲线C的参数方程为普通方程:(x-2)2+(y-1)2=9,
圆心(2,1)到直线x-3y+2=0的距离d=$\frac{|2-3+2|}{\sqrt{10}}$=$\frac{1}{\sqrt{10}}$<3,
直线和圆相交,过圆心和l平行的直线和圆的2个交点符合要求,
又$\frac{1}{\sqrt{10}}$+$\frac{{7\sqrt{10}}}{10}$<3
在直线l的另外一侧有圆上的2个点符合要求,
故答案为4
点评 解决这类问题首先把曲线C的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系得出结论.

练习册系列答案
相关题目
7.若A(6,-1,4),B(1,-2,1),C(4,2,3),则△ABC的形状是( )
| A. | 不等边锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 等边三角形 |
14.函数f(x)=1-2sin2x+2cos x的最小值和最大值分别为( )
| A. | -1,1 | B. | -$\frac{3}{2}$,-1 | C. | -$\frac{3}{2}$,3 | D. | -2,$\frac{3}{2}$ |
18.“B=60°”是“△ABC三个内角A、B、C成等差数列”的( )
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
8.已知y=$\frac{1}{3}{x^3}+b{x^2}$+(b+2)x+3是R上的单调函数,则b的取值范围是( )
| A. | -1≤b≤2 | B. | b≤-1或b≥2 | C. | -1<b<2 | D. | b<-1或b>2 |
12.集合A={x|x2-5x+4≤0},B={x||2x-3|≤3},则A∩B=( )
| A. | {x|0<x≤3} | B. | {x|1≤x≤3} | C. | {x|0≤x≤4} | D. | {x|1<x≤4} |
13.如果函数y=sinωx•cosωx(ω>0)的最小正周期为4π,那么常数ω为( )
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
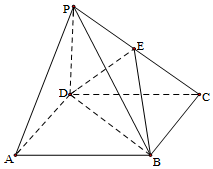 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.