题目内容
19.已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是( )| A. | (-∞,5) | B. | (-∞,5] | C. | (5,+∞) | D. | [5,+∞) |
分析 利用集合与充分不必要条件即可得出.
解答 解:集合A={x|x>5},集合B={x|x>a},
若命题“x∈A”是命题“x∈B”的充分不必要条件,
∴a<5,
则实数a的取值范围是(-∞,5).
故选:A.
点评 本题考查了集合与充分不必要条件,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.曲线f(x)=$\frac{lnx}{x}$在x=e处的切线方程为( )
| A. | y=e | B. | y=x-e+$\frac{1}{e}$ | C. | y=x | D. | y=$\frac{1}{e}$ |
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<0}\\{|\frac{1}{2}{x}^{2}-2x+1|,x≥0}\end{array}\right.$,方程f2(x)-af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
| A. | [6,11] | B. | [3,11] | C. | (6,11) | D. | (3,11) |
14.函数f(x)=1-2sin2x+2cos x的最小值和最大值分别为( )
| A. | -1,1 | B. | -$\frac{3}{2}$,-1 | C. | -$\frac{3}{2}$,3 | D. | -2,$\frac{3}{2}$ |
8.已知y=$\frac{1}{3}{x^3}+b{x^2}$+(b+2)x+3是R上的单调函数,则b的取值范围是( )
| A. | -1≤b≤2 | B. | b≤-1或b≥2 | C. | -1<b<2 | D. | b<-1或b>2 |
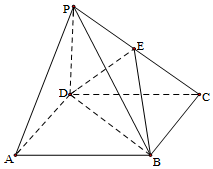 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.