题目内容
1.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-m),且$\overrightarrow{a}⊥\overrightarrow{b}$,则$|\overrightarrow a+\overrightarrow b|$=$\sqrt{10}$.分析 根据$\overrightarrow{a}⊥\overrightarrow{b}$便可得出$\overrightarrow{a}•\overrightarrow{b}=0$,从而求出m=1,进而可求出$\overrightarrow{a}+\overrightarrow{b}$的坐标,从而求出$|\overrightarrow{a}+\overrightarrow{b}|$的值.
解答 解:∵$\overrightarrow{a}⊥\overrightarrow{b}$;
∴$\overrightarrow{a}•\overrightarrow{b}=2-2m=0$;
∴m=1;
∴$\overrightarrow{a}+\overrightarrow{b}=(3,1)$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 考查向量垂直的充要条件,以及向量坐标的加法运算,根据向量坐标求向量长度的公式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.集合A={x|x2-5x+4≤0},B={x||2x-3|≤3},则A∩B=( )
| A. | {x|0<x≤3} | B. | {x|1≤x≤3} | C. | {x|0≤x≤4} | D. | {x|1<x≤4} |
16.过x轴上一点P作x轴的垂线,分别交函数y=sinx,y=cosx,y=tanx的图象于P1,P2,P3,若$\overrightarrow{P{P_3}}=\frac{3}{8}\overrightarrow{P{P_2}}$,则$|\overrightarrow{P{P_1}}|$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
13.如果函数y=sinωx•cosωx(ω>0)的最小正周期为4π,那么常数ω为( )
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
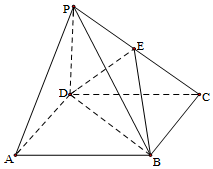 在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
在四棱锥P-ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.