Question

1．椭圆$\frac{x^2}{12}+\frac{y^2}{4}=1$的左、右焦点分别为F₁，F₂，过焦点F₁的直线交该椭圆于A，B两点，若△ABF₂的内切圆面积为π，A，B两点的坐标分别为（x₁，y₁），（x₂，y₂），则|y₁-y₂|的值为$\sqrt{6}$．

Answer 1

分析 由已知△ABF₂内切圆半径r=1，从而求出△ABF₂面积，再由ABF₂面积=$\frac{1}{2}$|y₁-y₂|×2c，能求出|y₁-y₂|．

解答 解：∵椭圆$\frac{x^2}{12}+\frac{y^2}{4}=1$的左右焦点分别为F₁，F₂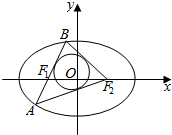，a=2$\sqrt{3}$，b=2，c=2$\sqrt{2}$，
过焦点F₁的直线交椭圆于A（x₁，y₁），B（x₂，y₂）两点，
△ABF₂的内切圆的面积为π，
∴△ABF₂内切圆半径r=1．
△ABF₂面积S=$\frac{1}{2}$×1×（AB+AF₂+BF₂）=2a=4$\sqrt{3}$，
∴ABF₂面积S=$\frac{1}{2}$|y₁-y₂|×2c=$\frac{1}{2}$|y₁-y₂|×2×2$\sqrt{2}$=4$\sqrt{3}$，
∴|y₁-y₂|=$\sqrt{6}$．
故答案为：$\sqrt{6}$．

点评 本题给出椭圆经过左焦点F₁的弦AB，在已知△ABF₂的内切圆的面积情况下，求A、B两点的纵坐标之差．着重考查了椭圆的定义、三角形内切圆的性质和三角形的面积公式等知识，属于中档题．