题目内容
已知圆C的方程为x2+（y-4）2=4，点O是坐标原点．直线l：y=kx与圆C交于M，N两点．
（Ⅰ）求k的取值范围；
（Ⅱ）过（1，3）点作圆的弦，求最小弦长？
（Ⅰ）求k的取值范围；
（Ⅱ）过（1，3）点作圆的弦，求最小弦长？
考点：直线与圆相交的性质
专题：直线与圆
分析：（Ⅰ）根据直线l与圆相交，得到圆心到直线l的距离d小于半径，即可求出k的取值范围；
（Ⅱ）当圆心与（1，3）连线为弦心距时，弦长最小，利用两点间的距离公式求出弦心距，由垂径定理及勾股定理求出最小弦长即可．
（Ⅱ）当圆心与（1，3）连线为弦心距时，弦长最小，利用两点间的距离公式求出弦心距，由垂径定理及勾股定理求出最小弦长即可．
解答：
解：（I）由圆的方程得：圆心C（0，4），半径r=2，
∵直线l与圆C相交于M，N两点，
∴圆心（0，4）到直线kx-y=0的距离d=
＜2，
整理得：1+k2＞4，即k2＞3，
解得：k＞
或k＜-
；
（II）当圆心与（1，3）连线为弦心距时，弦长最小，
∵圆心C到（1，3）的距离为
=
，半径r=2，
根据题意得：最小弦长为2
=2
．
∵直线l与圆C相交于M，N两点，
∴圆心（0，4）到直线kx-y=0的距离d=
| |-4| | ||
|
整理得：1+k2＞4，即k2＞3，
解得：k＞
| 3 |
| 3 |
（II）当圆心与（1，3）连线为弦心距时，弦长最小，
∵圆心C到（1，3）的距离为
| (1-0)2+(3-4)2 |
| 2 |
根据题意得：最小弦长为2
22-(
|
| 2 |
点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，点到直线的距离公式，两点间的距离公式，垂径定理，以及勾股定理，熟练掌握公式及定理是解本题的关键．
练习册系列答案
相关题目
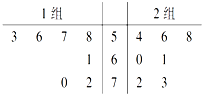如图是1，2两组各7名同学体重（单位：kg）数据的茎叶图．设1，2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若tanθ=2，则2sin2θ-sinθcosθ-cos2θ=（ ）
| A、5 | ||
| B、1 | ||
C、
| ||
D、
|