题目内容
圆C:x2+y2-2x-2y-7=0,设P是该圆的过点(3,3)的弦的中点,则动点P的轨迹方程是 .
考点:轨迹方程
专题:计算题,直线与圆
分析:由题意求出圆C的圆心为C(1,1),设A(3,3),由垂径定理得PC⊥AP,可得点P在以AC为直径的圆上运动.根据两点间的距离公式与中点坐标公式,求出以AC为直径的圆的圆心为B(2,2)、半径R=
,得到其方程为为(x-2)2+(y-2)2=2,即为动点P的轨迹方程.
| 2 |
解答:
解:∵圆C:x2+y2-2x-2y-7=0,化成标准方程得(x-1)2+(y-1)2=9,
∴圆心为C(1,1),半径r=3.
设A(3,3),连结PC
∵P是该圆的过点(3,3)的弦的中点,
∴PC⊥AP,可得点P在以AC为直径的圆上运动.
∵|AC|=
=2
,AC的中点为B(2,2)
∴以AC为直径的圆的圆心为B(2,2),半径R=
|AC|=
,
其方程为(x-2)2+(y-2)2=2,即为动点P的轨迹方程.
故答案为:(x-2)2+(y-2)2=2

∴圆心为C(1,1),半径r=3.
设A(3,3),连结PC
∵P是该圆的过点(3,3)的弦的中点,
∴PC⊥AP,可得点P在以AC为直径的圆上运动.
∵|AC|=
| (3-1)2+(3-1)2 |
| 2 |
∴以AC为直径的圆的圆心为B(2,2),半径R=
| 1 |
| 2 |
| 2 |
其方程为(x-2)2+(y-2)2=2,即为动点P的轨迹方程.
故答案为:(x-2)2+(y-2)2=2
点评:本题给出经过定点的直线与已知圆相交,求截得弦的中点轨迹方程.着重考查了垂径定理、两点间的距离公式和中点坐标公式等知识,考查了轨迹方程的求法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图是一个正三角形场地,如果在每边上放2盆花共需要3盆花;如果在每边上放3盆花共需要6盆花,如果在每边上放n(n>1)盆花,那么共需要花( )盆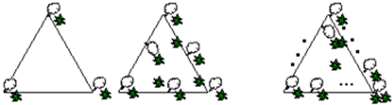

| A、3n | B、3n-1 |
| C、3n-2 | D、3n-3 |
 如图,正三棱柱ABC-A1B1C1的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为
如图,正三棱柱ABC-A1B1C1的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为