题目内容
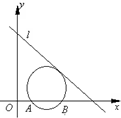 已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.
已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.(Ⅰ)求圆C的标准方程;
(Ⅱ)设P为l上的动点,求∠APB的最大值,以及此时P点坐标.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(Ⅰ)由题知,设圆心C(2,b),b>0,半径为r,利用圆C经过A(1,0)、B(3,0)两点,且与直线l相切,建立方程组,求出圆心与半径,即可求圆C的标准方程;
(Ⅱ)令圆C与直线l相切于P0点,由平面几何知识可知∠APB<∠AQB=∠AP0B,所以P取切点P0时,∠APB取得最大值,求出切点坐标,即可得出结论.
(Ⅱ)令圆C与直线l相切于P0点,由平面几何知识可知∠APB<∠AQB=∠AP0B,所以P取切点P0时,∠APB取得最大值,求出切点坐标,即可得出结论.
解答:
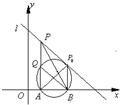 解:(Ⅰ)由题知,设圆心C(2,b),b>0,半径为r,
解:(Ⅰ)由题知,设圆心C(2,b),b>0,半径为r,
则
,解得
,
所以圆C的标准方程为:(x-2)2+(y-1)2=2; …(4分)
(Ⅱ)如图,令圆C与直线l相切于P0点,由平面几何知识可知∠APB<∠AQB=∠AP0B,所以P取切点P0时,∠APB取得最大值,…(6分)
由C(2,1),可得直线lCP0:y=x-1,由
解得P0(3,2),
又△AP0B为等腰直角三角形,则∠AP0B=45°,
所以∠APB最大值为45°,此时P点坐标为(3,2).…(8分)
 解:(Ⅰ)由题知,设圆心C(2,b),b>0,半径为r,
解:(Ⅰ)由题知,设圆心C(2,b),b>0,半径为r,则
|
|
所以圆C的标准方程为:(x-2)2+(y-1)2=2; …(4分)
(Ⅱ)如图,令圆C与直线l相切于P0点,由平面几何知识可知∠APB<∠AQB=∠AP0B,所以P取切点P0时,∠APB取得最大值,…(6分)
由C(2,1),可得直线lCP0:y=x-1,由
|
又△AP0B为等腰直角三角形,则∠AP0B=45°,
所以∠APB最大值为45°,此时P点坐标为(3,2).…(8分)
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )
用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )| A、120 | B、160 |
| C、180 | D、240 |
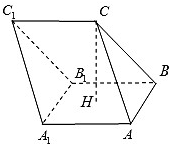 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.