题目内容
从正方体的各个棱面上的12条面对角线中任取两条,设ξ为两条面对角线所成的角(用弧度制表示),如当两条面对角线垂直时,ξ=
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
| π |
| 2 |
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)当ξ=0时,即所选的两条面对角线平行,由此能求出P(ξ=0).
(Ⅱ)由题意知ξ=0,
,
,分别求出P(ξ=0),P(ξ=
),P(ξ=
),由此能求出ξ的分布列和数学期望.
(Ⅱ)由题意知ξ=0,
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
解:(Ⅰ)当ξ=0时,即所选的两条面对角线平行.
则P(ξ=0)=
=
.(4分)
(Ⅱ)由题意知ξ=0,
,
,
P(ξ=0)=
=
,
P(ξ=
)=
=
,
P(ξ=
)=
=
,
∴ξ的分布列为:
(10分)
Eξ=0×
+
×
+
×
=
.(12分)
则P(ξ=0)=
| 6 | ||||
|
| 1 |
| 11 |
(Ⅱ)由题意知ξ=0,
| π |
| 3 |
| π |
| 2 |
P(ξ=0)=
| 6 | ||||
|
| 1 |
| 11 |
P(ξ=
| π |
| 3 |
| 48 | ||
|
| 8 |
| 11 |
P(ξ=
| π |
| 2 |
| 12 | ||
|
| 2 |
| 11 |
∴ξ的分布列为:
| ξ | 0 |
|
| ||||||
| P |
|
|
|
Eξ=0×
| 1 |
| 11 |
| π |
| 3 |
| 8 |
| 11 |
| π |
| 2 |
| 2 |
| 11 |
| π |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是历年高考的必考题型之一,解题时要注意排列组合知识的灵活运用,是中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若cos(π+α)=-
,则cosα的值为( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
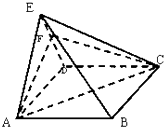 如图,在四棱锥E-ABCD中,底面ABCD为边长为5的正方形,AE⊥平面CDE,AE=3.
如图,在四棱锥E-ABCD中,底面ABCD为边长为5的正方形,AE⊥平面CDE,AE=3.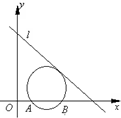 已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.
已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限. 在如图所示的三棱柱中,点A、BB1的中点M以及B1C1的中点N所确定的平面把三棱柱切割成体积不相等的两部分,则小部分的体积与大部分的体积之比为
在如图所示的三棱柱中,点A、BB1的中点M以及B1C1的中点N所确定的平面把三棱柱切割成体积不相等的两部分,则小部分的体积与大部分的体积之比为