题目内容
在平面直角坐标系中,已知平行四边形ABCD的三个顶点分别是A(-1,-2),B(0,1),C(3,2).
①求直线BC的方程;
②求平行四边形ABCD的面积.
①求直线BC的方程;
②求平行四边形ABCD的面积.
考点:点到直线的距离公式,直线的两点式方程
专题:直线与圆
分析:①由B(0,1),C(3,2),利用直线的两点式方程能求出直线BC的方程.
②由A(-1,-2),B(0,1),C(3,2)和直线BC的方程,能求出点A到直线BC的距离和BC的长,由此能求出S△ABC,从而能求出平行四边形ABCD的面积.
②由A(-1,-2),B(0,1),C(3,2)和直线BC的方程,能求出点A到直线BC的距离和BC的长,由此能求出S△ABC,从而能求出平行四边形ABCD的面积.
解答:
解:①∵B(0,1),C(3,2),
∴由直线的两点式方程得
直线BC的方程是
=
,
整理,得x-3y+3=0.
②∵A(-1,-2),B(0,1),C(3,2),直线BC的方程是x-3y+3=0,
∴点A到直线BC的距离d=
=
,
BC=
=
,
∴S△ABC=
×BC×d=
×
×
=4,
∴平行四边形ABCD的面积S=2S△ABC=2×4=8.
∴由直线的两点式方程得
直线BC的方程是
| y-1 |
| 2-1 |
| x-0 |
| 3-0 |
整理,得x-3y+3=0.
②∵A(-1,-2),B(0,1),C(3,2),直线BC的方程是x-3y+3=0,
∴点A到直线BC的距离d=
| |-1+6+3| | ||
|
4
| ||
| 5 |
BC=
| 32+(2-1)2 |
| 10 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 5 |
| 10 |
∴平行四边形ABCD的面积S=2S△ABC=2×4=8.
点评:本题考查直线方程的求法,考查四边形面积的求法,解题时要认真审题,注意两点式方程、点到直线距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,程序框图的输出结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
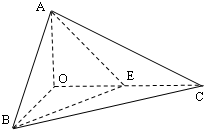 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4,
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4, 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示: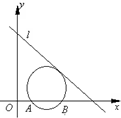 已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.
已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.